Tentukan pernyataan berikut benar atau salah a>b>c maka a>c

Matematika Comments Off on Tentukan pernyataan berikut benar atau salah a>b>c maka a>c 40 Views

Mapel Matematika, Jenjang Sekolah Menengah Atas

Jawab:

Benar, karena a>b>c (a lebih besar dari b dan lebih besar dari c), sehingga pasti a>c (a lebih besar dari c)

Pertanyaan Baru di Matematika

Math seorang anak berjalan sejauh 1.56 km. Anak itu akan menempuh jarak 2.14 km. Berapa Km lagi jarak yang harus ditempuh anak itu?
Gunakan cara
Jangan ngasal
Terimakasih
* Rara Ayuetha Alexa ( alexa )
* Phoenicia Jovanka ( vanka )

Matematika, Sekolah Menengah Atas

Jawaban:

Sisa jarak yg harus ditempuh

= jarak yg harus ditempuh – jarak yg telah di tempuh

= 2.14km – 1.56km

= 0.58km

= 580m

« Penyelesaian Soal »

[ Soal ]

Seorang anak berjalan sejauh 1.56 km. Anak itu akan menempuh jarak 2.14 km. Berapa Km lagi jarak yang harus ditempuh anak itu?

________________

✡ Cara Singkat

Sisa jarak = Jarak yang ditempuh – Jarak yang sudah Ditempuh

Sisa jarak = 2,14 km – 1,56 km
Sisa jarak = 0,58 km ☑

✡ Cara Panjang

• Mengubah Semua Satuan menjadi Cm

1 km = 100.000 cm

1,56 km
= ( 1,56 × 100.000 cm )
= 156.000 cm

2,14 km
= ( 2,14 × 100.000 cm )
= 214.000 cm

• Menentukan Sisa Jarak Yang Ditempuh

Sisa jarak = Jarak yang ditempuh – Jarak yang sudah Ditempuh

Sisa Jarak = 214.000 cm – 156.000 cm
Sisa Jarak = 58.000 cm

• Mengubah Satuan Cm menjadi Km

1 km = 100.000 cm

( Km ) = Jarak ÷ 100.000 cm
( Km ) = 58.000 cm ÷ 100.000 cm
( Km ) = 0,58 km ☑

Kesimpulan ☚

Maka, Sisa Jarak yang harus ditempuh Anak Tersebut adalah 0,58 km ☑

Detail jawaban ☛☚

Kelas : 5/SD
Mapel : Matematika
Materi : Satuan Jarak
Kode soal : 2
Kode kategorisasi : 5.2.1
Kata Kunci : Sisa, Jarak, Yang ditempuh

Semoga Bisa Bermanfaat-!

Tlg ya…. nanti yang jawaban paling bagus di follow dan di jadikan yg terbaik

Matematika, Sekolah Menengah Pertama

Penjelasan dengan langkah-langkah:

1) kalikan

3(x-2) + x + 5 = 2x

3x – 6 + x + 5 = 2x

4x – 2x – 1 = 0

2x = 1

x = 1/2 = ½

2) kalikan 30

5x – 6 (x-14) = 20x

5x – 6x + 84 = 20 x

-x + 84 = 20x

84 = 21x

4 = x

3) kalikan 12

4x + 2 = x – 6

4x – x = -6-2

3x = -8

x = -8/3

4) kalikan 30

18x – 15 = 20x + 5

18x – 20x = 5 + 15

-2x = 20

x = -10

5) kalikan 6

2(x-1) – (2x+3) = 6x – 6

2x – 2 – 2x – 3 = 6x – 6

-5 + 6 = 6x

1 = 6x

1/6 = x

( 1 )

( 2 )

( 3 )

( 4 )

( 5 )

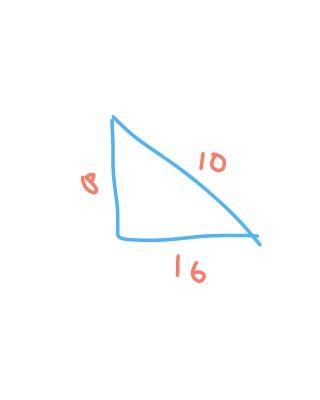
Alas sebuah segitiga = 16cm tinggi segitiga = 8cm
sisi miring = 10cm
Hitunglah luas dan keliling bangun tersebut!
bantu jawab:((plis

Matematika, Sekolah Dasar

Penjelasan dengan langkah-langkah:

maka :

a. luas

L = 1/2 × a × t

L = 1/2 × 16 × 8

L = 16/2 × 8

L = 8 × 8

L = 64 cm²

b.keliling

k = s1 + s2 + s3

k = 16 + 8 + 10

k = 24 + 10

k = 34 cm

Penjelasan dengan langkah-langkah:

luas

½ × a × t
½ × 16 × 8
8 × 8
64 cm²

keliling

a + b + c
8 + 10 + 16
26 + 8
34cm

Q. ( bil. bulat )
1) 100 ÷ 50 × 21 + 27 = ..?

2) 21 + 21 ( 5 × 5 ) – 21 ÷ 3 = ..?

≈ Pakai cara!
≈ ngasal⬄report!
≈ Rapi!
≈ Cara susun⬄beA!
≈ Salah⬄koreksi 30 menit!

————————————

25+

Matematika, Sekolah Menengah Pertama

Penyelesaian :

—–

Ingat aturan operasi dalam matematika!

– Prioritas pertama : Operasi dalam kurung (dari kiri ke kanan)

– Prioritas kedua : Operasi pangkat dan akar (dari kiri ke kanan)

– Prioritas ketiga : Operasi perkalian dan pembagian (dari kiri ke kanan)

– Prioritas keempat : Operasi penjumlahan dan pengurangan (dari kiri ke kanan)

—–

Soal nomor 1

100 ÷ 50 × 21 + 27

Operasikan pembagian di kiri

2 × 21 + 27

Operasikan perkalian yang tersisa

42 + 27

Operasikan penjumlahan yang ada

= 69

—–

Soal nomor 2

21 + 21 . ( 5 × 5 ) – 21 ÷ 3

Operasikan perkalian dalam kurung

21 + 21 × 25 – 21 ÷ 3

Operasikan perkalian dan pembagian

21 + 525 – 7

Operasikan penjumlahan dan pengurangan

= 539

Q.

___________________________________________

100 ÷ 50 × 21 + 27

= 2 × 21 + 27

= 42 + 27

= 69

___________________________________________

21 + 21(5 × 5) – 21 ÷ 3

= 21 + 21(25) – 21 ÷ 3

= 21 + 525 – 21 ÷ 3

= 21 + 525 – 7

= 21 + 518

= 539

___________________________________________