Tentukan banyak garis yang dapat dibuat dari 4 titik non kolinear tidak sejajar yang tersedia

Tentukan banyak garis yang dapat dibuat dari 4 titik non kolinear tidak sejajar yang tersedia​

Mapel Matematika, Jenjang Sekolah Menengah Pertama

dari n buah titik yang nonkolinear (tidak segaris) dapat dibuat sebanyak

n(n – 1)/2 garis

maka dari 4 titik nonkolinear dapat dibuat sebanyak

= 4(4 – 1)/2

= 6 garis

Pertanyaan Baru di Matematika

---

Lum menemukan jawabn nie gmn ea langkahnya, 37x15x14=
32x19x17=
45x7x32=
Tolong dong

Matematika, Sekolah Dasar

Jawaban :

1 . 37 X 15 X 14 = 7,770

2 . 32 X 19 X 17 = 10,336

3 . 45 X 7 X 32 = 10,080

Jangan lupa kasih rate & like yahh trmksh

---

Sebutkan dan berikan contoh 10 himpunan bilangan​

Matematika, Sekolah Menengah Pertama

Jawab:

Penjelasan dengan langkah-langkah:

1) Himpunan Bilangan Kompleks

2) Himpunan Bilangan Real

3) Himpunan Bilangan Rasional

4) Himpunan Bilangan Irasional

5) Himpunan Bilangan Bulat

6) Himpunan Bilangan Asli

7) Himpunan Bilangan Prima

8) Himpunan Bilangan Genap

9) Himpunan Bilangan Ganjil

10) Himpunan Bilangan Transendental

---

5 – 3
3 + (-5)
-5 -3
Tolong ya kaaa pakai garis bilangann

Matematika, Sekolah Menengah Atas

Jawaban:

2

-2

-8

semoga bermanfaat

---

Tentukan warna apakah untuk bilangan 3.426…​

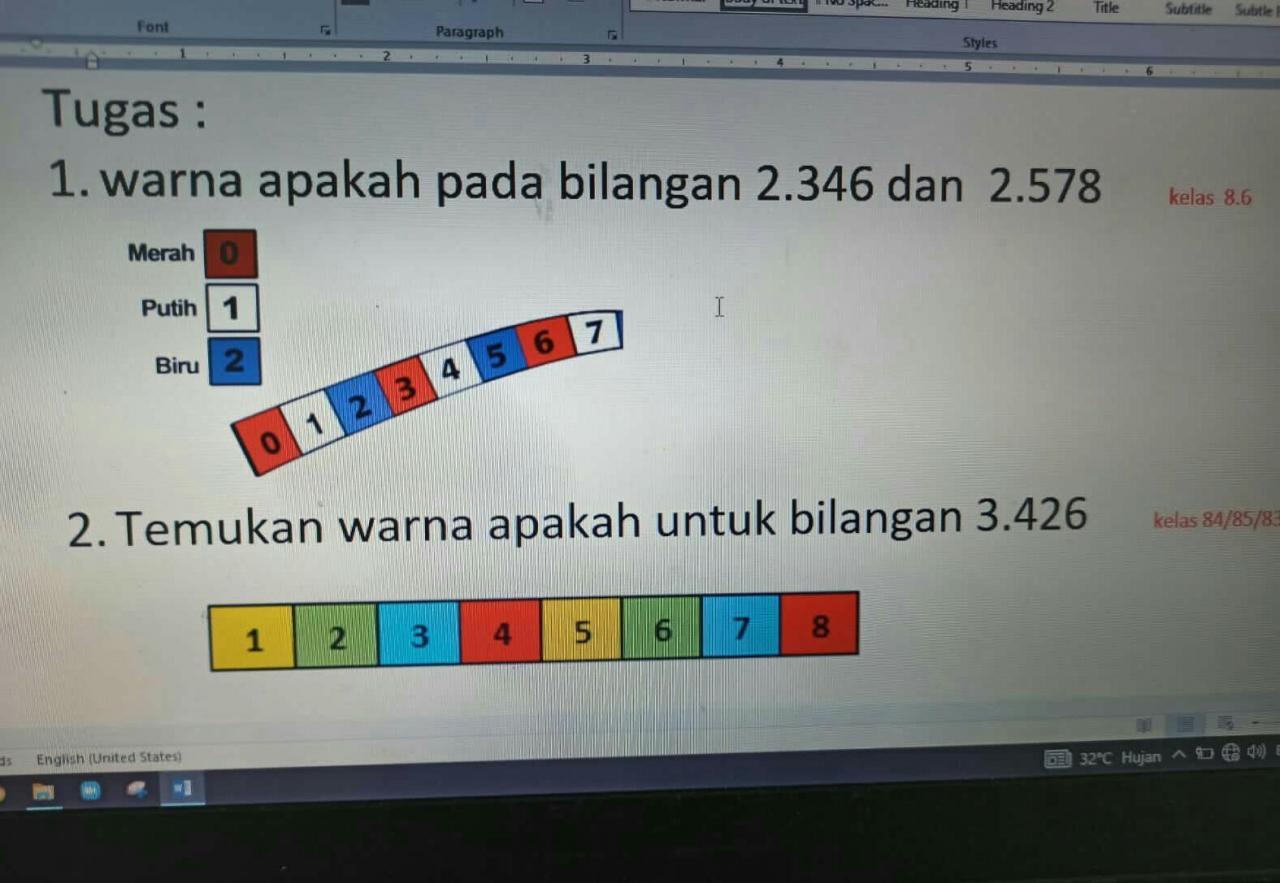
Matematika, Sekolah Menengah Pertama

Nomor 1)

warna bilangan 2.346 adalah biru, jingga, putih, jingga

warna bilangan 2.578 adalah biru, biru, putih, jingga

Nomor 2)

warna bilangan 3.426 adalah biru muda, jingga, hijau pupus, hijau pupus

---

20 + (- 18) + 8 ……

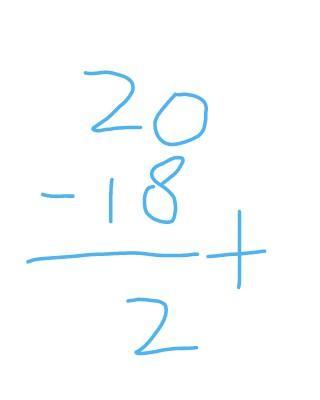
Matematika, Sekolah Dasar

Jawaban:

___________

20 + (-18) + 8

= 2 + 8

= 10

___________

Jawaban :

20 + ( – 18 ) + 8 = ......

Adalah

10

caranya hitung angka didepannya yg lebih besar, jika positif yg lebih besar maka dikurangi dengan negatif.

Tambahan pengertian dari nana :

( + ) + ( – ) = +/– sesuai dengan angka yg lebih besar , Jadi jawaban nya bisa positif atau negatif sesuai dengan angka nya yg LEBIH BESAR atau LEBIH KECIL