Seorang pejabat direktorat jenderal pajak menduga bahwa prosentase wajib pajak yang belum membayar pajak kurang dari 40%. Untuk membuktikan dugaan tersebut, diambil sampel acak sebanyak 18 orang dan ternyata ada 6 orang yang belum membayar pajak. Dengan taraf nyata 5%, apakah dugaan tersebut benar?.

Seorang pejabat direktorat jenderal pajak menduga bahwa prosentase wajib pajak yang belum membayar pajak kurang dari 40%. Untuk membuktikan dugaan tersebut, diambil sampel acak sebanyak 18 orang dan ternyata ada 6 orang yang belum membayar pajak. Dengan taraf nyata 5%, apakah dugaan tersebut benar?.

Mapel Matematika, Jenjang Sekolah Menengah Pertama

Dengan menggunakan taraf 5%, dugaan bahwa persentase wajib pajak yang belum membayarkan pajak kurang dari 40% adalah tidak benar. Hal ini dibuktikan dengan hasil bahwa kita menerima H₀ dan menolak H₁ (klaim).

Penjelasan dengan langkah-langkah:

Diketahui:

Hipotesis:

H₀: p = 40%

H₁: p < 40% (klaim)

n = 18

x = 6

= 5%

dimana p = proporsi WP yang belum membayar pajak

Ditanya:

Apakah dugaan tersebut benar?

Pembahasan:

1. Cari p = proporsi

p = x/n

p = 6/18

p = 0,33

dan

q = 1-p

q = 1-0,33

q = 0,67

2. Uji populasi

• Cari dulu  :

=

=

= 0,115

• Kemudian cari

=

=

= -0,580

Karena t kritis pada saat n = 18 dan = 5% adalah 1,740 atau -1,740. Sehingga > t yaitu -0,58 > -1,74. Maka dari itu kesimpulannya adalah menerima H₀ dan menolak H₁ yang menyatakan bahwa persentase WP yang belum bayar pajak adalah kurang dari 40%.

Pelajari lebih lanjut

Materi tentang Merumuskan Hipotesis untuk Suatu Penelitian pada

#BelajarBersamaBrainly #SPJ1

Pertanyaan Baru di Matematika

---

Q.

1.) 858×44=
2.) 343×33=
3.) 6565×23=​

Matematika, Sekolah Menengah Pertama

Penjelasan dengan langkah-langkah:

cara beserta jawaban terlampir yaak

Jawaban:

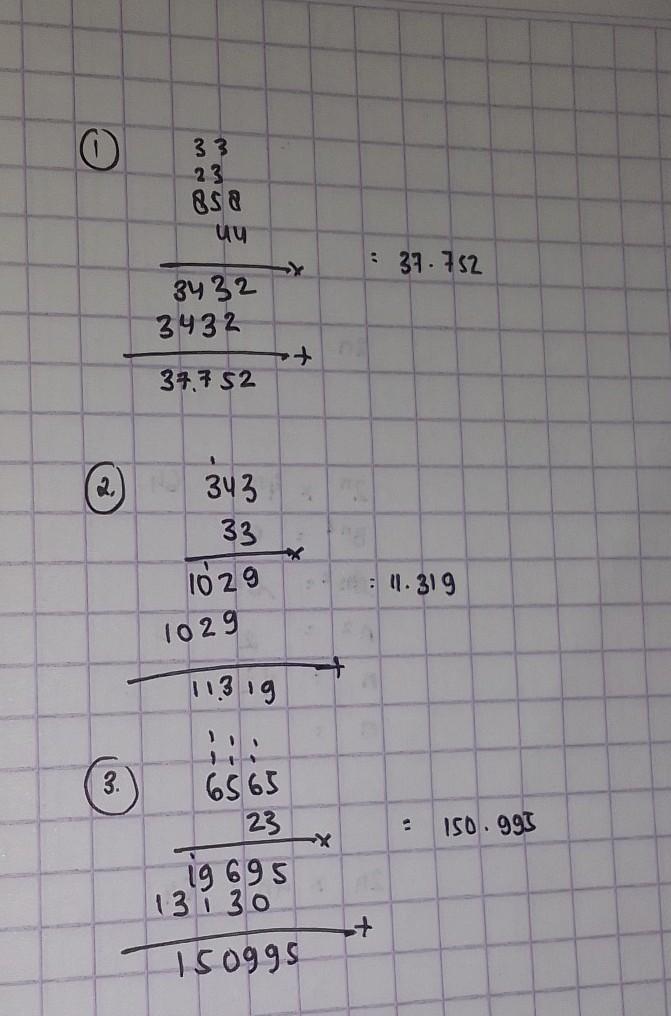
1). 858 × 44 = 37.752

• Penyelesaian :

>> 858

44

____________×

3432

3432

____________+

37752

2). 343 × 33 = 11.319

• Penyelesaian :

>> 343

33

____________×

1029

1029

____________+

11.319

3). 6.565 × 23 = 150.995

• Penyelesaian :

>> 6565

23

_______________×

19695

13130

_______________+

150995

---

A. nilai X
B. nilai sudut CBD ​

Matematika, Sekolah Menengah Pertama

Diketahui dua sudut dalam sepihak berjumlah 180°

A. 4x-4°+2x+7°=180°

6x+3°=180°

6x=180°-3°

6x=177°

x=29,5°

B. <CBQ

4x-4°

4(29,5)-4°

118°-4°

114°

<CBD+<CBQ=180°

<CBD+114°=180°

<CBD=180°-114°

<CBD=66°

---

Diketahui data dari 6 orang yang diwawancarai tentang pendapatan (X) dan pengeluaran (Y) perbulan dalam ribuan rupiah. Pendapatan (X) : 800 900 700 600 700 800Pengeluaran (Y) : 300 300 200 100 200 200Hitunglah koefisien korelasi product Moment dengan taraf signifikan 5%. ​.

Matematika, Sekolah Menengah Atas

Koefisien korelasi dari product moment adalah 0,886621. Hasil ini didapatkan dengan menggunakan rumus koefisien korelasi.

Penjelasan dengan langkah-langkah:

Diketahui:

X (pendapatan) = 800 900 700 600 700 800

Y (konsumsi)      = 300 300 200 100 200 200

taraf signifikan   = 5%

n = 6 orang

Ditanya:

Hitung koefisien korelasi!

Pembahasan:

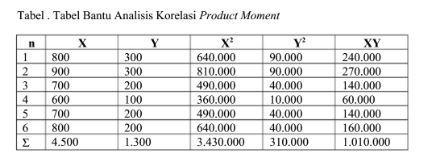
• Berdasarkan tabel bantu yg telah terlampir didapatkan nilai:

= 4.500

= 1.300

= 3.430.000

= 310.000

n = 6

• Hitung koefisien korelasi:

Sehingga diperoleh koefisien korelasi (r) yaitu 0,886621. Karena hasilnya positif dan mendekati angka 1 maka hubungan konsumsi dan pendapatan searah dan kuat yang mengandung arti bahwa peningkatan pendapatan seseorang akan diikuti oleh peningkatan pengeluaran/konsumsi.

Pelajari lebih lanjut

Materi tentangperbedaan koefisien korelasi dengan koefisien determinasi pada

#BelajarBersamaBrainly #SPJ1

---

4. Tentukan nilai lim x = π/2 cos x tan 2x / 2 sin x cos x 5. Tentukan nilai limit x= π/2 sin 5x + sin 3x / cos 5x + cos 3x
​

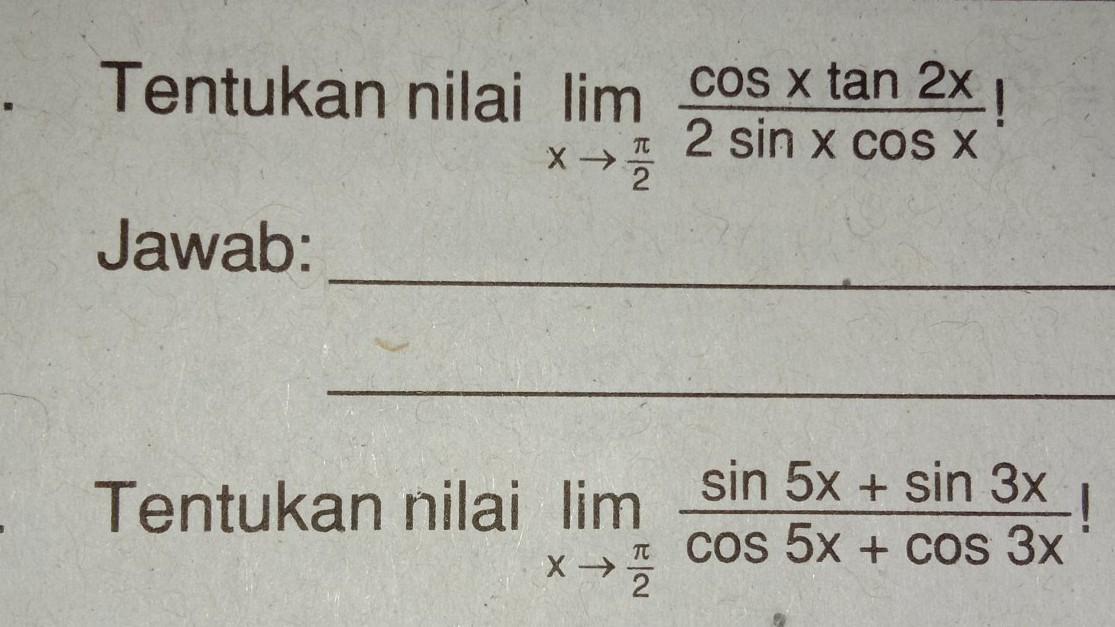
Matematika, Sekolah Menengah Atas

Penjelasan dengan langkah-langkah:

Nomor 4

Nomor 5

---

2 l =…………….cl

Matematika, Sekolah Dasar

Jawaban:

2l=200 cl

Penjelasan dengan langkah-langkah:

diketahui:

2 l =…………….cl

ditanya:

cl

jawab:

2l=…cl

cl=2×100

cl=200

=200 cl

2l=200 cl

semoga membantu (: