SEDERHANAKAN BENTUK BENTUK BERIKUT INI DAN NYATAKAN HASILNYA DALAM BENTUK PANGKAT BULAT POSITIF.

SEDERHANAKAN BENTUK BENTUK BERIKUT INI DAN NYATAKAN HASILNYA DALAM BENTUK PANGKAT BULAT POSITIF.​

Mapel Matematika, Jenjang Sekolah Menengah Pertama

A. (2-³ × 2^7) × 2^4

= (1/2³ × 2^7) × 1/2⁴

= (2^7/2⁴) × 1/2⁴

= 2⁴ × 1/2⁴

= 2⁴/2⁴

= 1

B. 3-⁴ × (3^-8 × 3^9)

= 1/3⁴ × (1/3^8 × 3^9)

= 1/3⁴ × (3^9/3^8)

= 1/3⁴ × 3¹

= 3¹/3⁴

= 1/3³

C. (0,13)⁴ × (0,13)^-6

= (0,13)⁴ × 1/0,13^6

= 0,13⁴/0,13^6

= 1/0,13²

D. (a⁴ × a^6) : a^15

= a^10 : a^15

= a^-5

= 1/a^5

E. (p²q-³)⁴ × p²q^6

= p^8q-¹² × p²q^6

= p^10q^-6

= p^10/q^6

F. -3x-² + x-¹ + 4x^0

= 1/-3x² + 1/x¹ + 4(1)

= 1/–3x² + 1/x¹ + 4

:)

✧ ☛ Pembahasan ☚ ✧

➩ Pengertian bilangan berpangkat

• Bilangan berpangkat adalah suatu bilangan yang bertujuan untuk menyederhanakan dalam suatu penulisan bilangan apabila dikali dengan bilangan yang sama.

➩ Rumus bilangan berpangkat

Keterangan :

➩ Jenis-jenis bilangan berpangkat

• Bilangan berpangkat positif
• Bilangan berpangkat negatif
• Bilangan berpangkat nol

➩ Macam – macam bilangan berpangkat

1. Bilangan berpangkat dua (Kuadrat)

• Bilangan berpangkat dua adalah suatu bilangan yang mengalikan bilangan utama sebanyak dua kali. Rumus bilangan berpangkat dua yaitu :

• Keterangan :

a = bilangan pokok atau absis

Contoh bilangan berpangkat dua yaitu :

1² = 1 × 1 = 1

2² = 2 × 2 = 4

3² = 3 × 3 = 9

4² = 4 × 4 = 16

5² = 5 × 5 = 25

6² = 6 × 6 = 36

7² = 7 × 7 = 49

8² = 8 × 8 = 64

9² = 9 × 9 = 81

10² = 10 × 10 = 100

2. Bilangan berpangkat tiga (Kubik)

• Bilangan berpangkat tiga adalah suatu bilangan yang mengalikan bilangan utama sebanyak tiga kali. Rumus bilangan berpangkat tiga yaitu :

• Keterangan :

a = bilangan pokok atau absis

Contoh bilangan berpangkat tiga yaitu :

1³ = 1 × 1 × 1 = 1

2³ = 2 × 2 × 2 = 8

3³ = 3 × 3 × 3 = 27

4³ = 4 × 4 × 4 = 64

5³ = 5 × 5 × 5 = 125

6³ = 6 × 6 × 6 = 216

7³ = 7 × 7 × 7 = 343

8³ = 8 × 8 × 8 = 512

9³ = 9 × 9 × 9 = 729

10³ = 10 × 10 × 10 = 1.000

➩ Sifat – sifat bilangan berpangkat

✧ ☛ Penyelesaian ☚ ✧

➩ Bagian A

➩ Bagian B

➩ Bagian C

➩ Bagian D

➩ Bagian E

➩ Bagian F

———————————————————–

Pelajari lebih banyak lagi tentang bilangan berpangkat yuk!

• Pengertian bilangan berpangkat :
• Hasil pangkat dari 1² sampai 50 pangkat 2 :
• Perpangkatan dan bentuk akar :

———————————————————–

Detail Jawaban

Kelas : 9 SMP

Mapel : Matematika

Materi : Bentuk Akar dan Pangkat

Kode Kategorisasi : 9.2.1

#BelajarBersamaBrainly

Pertanyaan Baru di Matematika

---

1(1) ÷ 2(2) × 3(3) – 4(4) + 5(5)
=========================

Sertakan cara penyelesaian y!

ty! Trms ^^

​

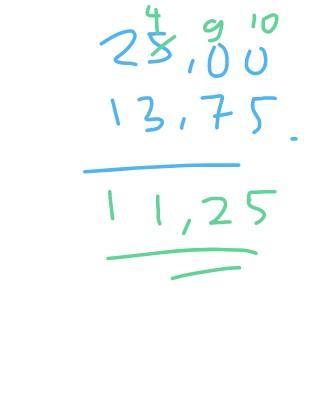
Matematika, Sekolah Menengah Pertama

Penjelasan dengan langkah-langkah:

1(1) ÷ 2(2) × 3(3) – 4(4) + 5(5)

1 ÷ 4 x 9 – 16 + 25

0,25 x 9 – 16 + 25

2,25 – 16 + 25

11,25

Jawaban:

1(1) ÷ 2(2) × 3(3) – 4(4) + 5(5)

= (1 × 1) ÷ 2(2) × 3(3) – 4(4) + 5(5)

= 1 ÷ 2(2) × 3(3) – 4(4) + 5(5)

= 1 ÷ (2 × 2) × 3(3) – 4(4) + 5(5)

= 1 ÷ 4 × 3(3) – 4(4) + 5(5)

= 0,25 × 3(3) – 4(4) + 5(5)

= 0,25 × (3 × 3) – 4(4) + 5(5)

= 0,25 × 9 – 4(4) + 5(5)

= 2,25 – 4(4) + 5(5)

= 2,25 – (4 × 4) + 5(5)

= 2,25 – 16 + 5(5)

= -13,75 + 5(5)

= -13,75 + (5 × 5)

= -13,75 + 25

= 11,25

---

Diyo membeli 2 gunting dan 3 spidol seharga rp39.000,00, sedangkan yuli membeli 3 gunting dan 5 spidol seharga rp62.500,00 di toko yang sama. nika membeli 4 gunting dan 2 spidol. jumlah uang yang harus dibayar nika adalah … .

Matematika, Sekolah Menengah Pertama

Penjelasan dengan langkah-langkah:

Materi : Matematika – Sistem Persamaan Linear Dua Variabel

Pertama, kita tentukan lambang variabel, yaitu x dan y

x = gunting

y = spidol

Lalu terjemahkan barang barang yang dibeli dengan menggunakan lambang variabel

2x + 3y = 39.000 (1)

3x + 5y = 62.500 (2)

Lalu kita kalikan secara terbalik dari variabel yang kita kalikan

2x + 3y = 39.000 x3

3x + 5y = 62.500 x2

Setelah dikalikan

6x + 9y = 117.000

6x + 10y = 125.000

lalu kita kurangkan

6x + 9y = 117.000

6x + 10y = 125.000 –

-1y = -8.000

y = 8.000

Sehingga nilai y (spidol) sebesar Rp. 8.000

Lalu masukan nilai 8.000 ke salah satu persamaan diatas contoh kita ambil persamaan ke 1

2x + 3y = 39.000

2x + (3×8.000) = 39.000

2x + 24.000 = 39.000

2x = 39.000 – 24.000

2x = 15.000

x = 15.000/2

x = 7.500

Jadi harga gunting sebesar Rp. 7.500

Lalu Nika membeli 4 gunting dan 2 spidol, kita lambangkan sebagai

4x + 2y

Lalu yang jadi masalah berapa harga yang harus dibayar untuk membeli 4 gunting dan 2 spidol?

Tinggal kita masukan harga gunting dan spidol yang sudah diperoleh, sehingga

(4 x 7.500) + (2 x 8.000) = 30.000 + 16.000 = 46.000

Jadi Nika harus membayar sebesar Rp. 46.000 untuk membeli 4 gunting dan 2 spidol.

Terima kasih

Referensi : Buku Matematika (Jurusan Akuntansi) Kelas 10 KTSP 2006 Penerbit Erlangga.

Semangat belajar !

---

Tolong kak makasih banyak ​

Matematika, Sekolah Menengah Pertama

Penyelesaian:

p³×p⁴

=p^3+4

=p^7

—————————————-

p^m×p^n=p^m+n

——————–

a^6÷a^2

=a^6-2

=a⁴

——————–

a^p÷a^q

=a^p-q

——————–

(m³)²

=m^3+2

=m^5

——————–

2^6×5²

=64×25

=1.600

=40^2

——————–

18³÷3^6

=5.832÷728

=8

=2^3

——————–

2^6÷3⁴

=64÷81

=8²÷9²

=(8/9)²

——————–

(a^5)³

=a^5+3

=a^8

——————–

7×2³+9×2³

=7×8+9×8

=8(7+9)

=7(16)

=128

=2^7

——————–

5×3^7+4×3^7

=3^7(5+4)

=3^7(9)

=3^7(3^2)

=3^9

——————–

8×5⁴-3×5⁴

=5⁴(8-3)

=5⁴(5)

=5^5

——————–

2³×5³

=(2×5)³

=10³

——————–

25³×8²

=5^6×2^6

=(2×5)^6

=10^6

——————–

27⁴÷6^8

=27⁴÷36⁴

=(27÷36)⁴

=(0,75)⁴

---

2 per 4 + 1 per 2 = ​

Matematika, Sekolah Menengah Atas

Jawab:

Penjelasan dengan langkah-langkah:

Disamakan bawahnya / dikecilkan juga bisa:

1. 2/4 + 1/2

= 1/2 + 1/2 = 1

2. 2/3 + 3/5

= 10/15 + 9/15

= 19/15

3. 2/5 + 1/2

= 4/10 + 5/10

= 9/10

4. 2/3 + 4/6

= 2/3 + 2/3

= 4/3

5, 6, dst nya gak ada keterangan + – jadi gak bisa jawab

---

Tentukan hasil haha ​

Matematika, Sekolah Menengah Pertama

5^-5 × 5²

= 1/5^5 × 5²

= 5²/5^5

= 1/5³

(2-¹ × 3²)²

= 2-² × 3⁴

= 1/2² × 3⁴

= 3⁴/2²

= 81/4

= 27

= 3³

(4-² × 2⁴)-²

= 4⁴ × 2^-8

= 4⁴ × 1/2^8

= 4⁴/2^8

= 256/256

= 1

🙂

• Hasil dari adalah
• Hasil dari adalah
• Hasil dari adalah

✧ ☛ Pembahasan ☚ ✧

➩ Pengertian bilangan berpangkat

• Bilangan berpangkat adalah suatu bilangan yang bertujuan untuk menyederhanakan dalam suatu penulisan bilangan apabila dikali dengan bilangan yang sama.

➩ Rumus bilangan berpangkat

Keterangan :

➩ Jenis-jenis bilangan berpangkat

• Bilangan berpangkat positif
• Bilangan berpangkat negatif
• Bilangan berpangkat nol

➩ Macam – macam bilangan berpangkat

1. Bilangan berpangkat dua (Kuadrat)

• Bilangan berpangkat dua adalah suatu bilangan yang mengalikan bilangan utama sebanyak dua kali. Rumus bilangan berpangkat dua yaitu :

• Keterangan :

a = bilangan pokok atau absis

Contoh bilangan berpangkat dua yaitu :

1² = 1 × 1 = 1

2² = 2 × 2 = 4

3² = 3 × 3 = 9

4² = 4 × 4 = 16

5² = 5 × 5 = 25

6² = 6 × 6 = 36

7² = 7 × 7 = 49

8² = 8 × 8 = 64

9² = 9 × 9 = 81

10² = 10 × 10 = 100

2. Bilangan berpangkat tiga (Kubik)

• Bilangan berpangkat tiga adalah suatu bilangan yang mengalikan bilangan utama sebanyak tiga kali. Rumus bilangan berpangkat tiga yaitu :

• Keterangan :

a = bilangan pokok atau absis

Contoh bilangan berpangkat tiga yaitu :

1³ = 1 × 1 × 1 = 1

2³ = 2 × 2 × 2 = 8

3³ = 3 × 3 × 3 = 27

4³ = 4 × 4 × 4 = 64

5³ = 5 × 5 × 5 = 125

6³ = 6 × 6 × 6 = 216

7³ = 7 × 7 × 7 = 343

8³ = 8 × 8 × 8 = 512

9³ = 9 × 9 × 9 = 729

10³ = 10 × 10 × 10 = 1.000

➩ Sifat – sifat bilangan berpangkat

✧ ☛ Penyelesaian ☚ ✧

➩ Nomor 1

➩ Nomor 2

➩ Nomor 3

———————————————————–

Pelajari lebih banyak lagi tentang bilangan berpangkat yuk!

• Pengertian bilangan berpangkat :
• Hasil pangkat dari 1² sampai 50 pangkat 2 :
• Perpangkatan dan bentuk akar :

———————————————————–

Detail Jawaban

Kelas : 9 SMP

Mapel : Matematika

Materi : Bentuk Akar dan Pangkat

Kode Kategorisasi : 9.2.1

#BelajarBersamaBrainly