Q
f(x) = x² × x³ + x × 3
f(5) =
nt : tampan ;_;

Mapel Matematika, Jenjang Sekolah Dasar
Jawaban:
Pembahasan
Diketahui
—
Ditanya
—
Dijawab
—-
Diketahui :
- f(x) = x² × x³ + x × 3
Ditanya :
- f(5) = ?
Jawab :
Kesimpulan :
- Jadi, hasil dari
Pertanyaan Baru di Matematika
2 1/4 + 3 5/6
Ini pecahan campuran ya
Matematika, Sekolah Dasar
2 1/4 + 3 5/6
= 5/4 + 23/6
= 15/12 + 46/12
= 61/12
= 5 1/12
Berapakah hasil dari

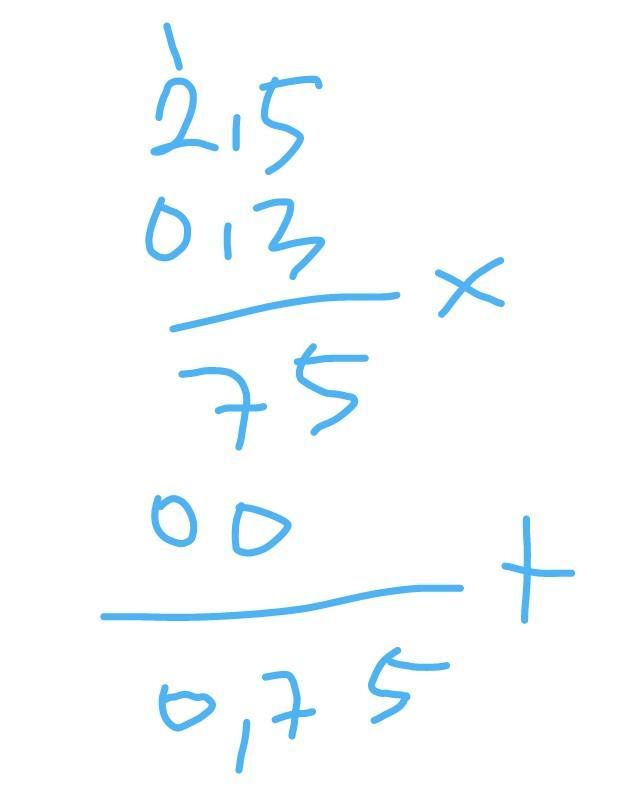
Matematika, Sekolah Menengah Pertama
Penjelasan dengan langkah-langkah:
- 2.5 × 0,3
- 0.75
semoga membantu
Langkah–langka :
✎ Cara ke-2
Q:) 
Diketahui 2x + 2y × 3x – 3y, maka ditanyakan
x → 27 dan y → 37 adalah …
a. 3.759
b. 7.395
c. 5.937
d. Tidak ada di opsi


≈ Sertakan cara penyelesaian!
≈ ngasal → report!
≈ Rapi!
≈ Salah → koreksi!
≈ grade 3/5 dijamin beA!

kangen :)
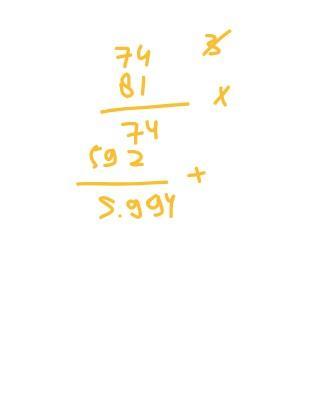
Matematika, Sekolah Menengah Pertama
x = 27
y = 37
2x + 2y × 3x – 3y
= 2x + 6xy – 3y
= 2(27) + 6(27)(37) – 3(37)
= 54 + 162(37) – 111
= 54 + 5.994 – 111
= 6.048 – 111
= 5.937
Jawaban C
Diketahui 2x + 2y × 3x – 3y, maka ditanyakan
x → 27 dan y → 37 adalah …
a. 3.759
b. 7.395
c. 5.937
d. Tidak ada di opsi
Pembahasan
→ Diketahui :
x 27
y 37
• – – – – • – – – – • – – – – •
→ Ditanyakan :
hasil dari 2x + 2y × 3x – 3y adalah?
• – – – – • – – – – • – – – – •
→ Penyelesaian :
2x + 2y × 3x – 3y
= 2(27) + 2(37) × 3(27) – 3(37)
= (2 × 27) + 2(37) × 3(27) – 3(37)
= 54 + (2 × 37) × 3(27) – 3(37)
= 54 + 74 × (3 × 27) – 3(37)
= 54 + 74 × 81 – (3 × 37)
= 54 + 74 × 81 – 111
= 54 + (74 × 81) – 111
= 54 + 5.994 – 111
= 6.048 – 111
=
• – – – – • – – – – • – – – – •
Kesimpulan
Jadi hasil dari 2x + 2y × 3x – 3y, jika x → 27 dan y → 37 adalah 5.937. opsi C.
• – – – – • – – – – • – – – – •
∂єтαιℓ נαωαвαη ꕤ ─ ✉
- Mapel : Matematika
- Kelas : 8
- Materi : Bab 2 – Fungsi
- Kode Mapel : 2
- Kode Kategori : 8.2.2
Kata Kunci : Tentukan hasil dari 2x + 2y × 3x – 3y, Jika x → 27 dan y → 37.
• – – – – • – – – – • – – – – •
Catatan:
- Maaf 🙂 detail jawaban nya nggak nyambung :v
#BelajarBersamaBrainly
-2 ½ buat menjadi pecahan biasa
Matematika, Sekolah Menengah Pertama
Jawaban:
PECAHAN BIASA
=(2×2+1/2
=(4+1)1/2
=5/2
BENTUK DESIMAL
5/2
=(5×50)/2×50
=250/100
=25/10
=2,5
BENTUK PERSEN
5/2×100 %
=500 % 10 / 2
=250 %
Penjelasan dengan langkah-langkah:
DIATAS ADA PENJELASAN MAAF KALAU SALAH ,SEMOGA BERMANFAAT
Jawab: 5/2
Penjelasan dengan langkah-langkah: 2 x 2 = 4 + 1 = 5 karna penyebut tidak dapat dirubah, jadi penyebutnya tetap 2 sehingga hasilnya menjadi 5/2
jawaban tercerdasnya kak 🙂
Perbandingan banyaknya uang pak Wisnu : pak Heri =7:5 sedangkan selisi uang mereka Rp 2.500.000 uang pak heri
Matematika, Sekolah Menengah Pertama
Perbandingan banyaknya uang Pak Wisnu : Pak Heri = 7 : 5. Sedangkan selisih uang mereka Rp 2.500.000. Maka uang Pak Heri sebesar
Pembahasan
Diketahui :
Pak Wisnu : Pak Heri = 7 : 5
Selisih uang = Rp2.500.000
• – – – – • – – – – • – – – – •
Ditanyakan :
Besar uang Pak Heri?
• – – – – • – – – – • – – – – •
Penyelesaian :
Uang Pak Heri
5/(7 – 5) × Rp2.500.000
= 5/2 × Rp2.500.000
= 5 × Rp1.250.000
=
• – – – – • – – – – • – – – – •
Kesimpulan
Jadi, besar uang Pak Heri adalah Rp6.250.000.
• – – – – • – – – – • – – – – •
∂єтαιℓ נαωαвαη ꕤ ─ ✉
- Mapel : Matematika
- Kelas : 6
- Materi : Bab 9 – Perbandingan
- Kode Mapel : 2
- Kode Kategori : 6.2.9
Kata Kunci : Perbandingan banyaknya uang pak Wisnu : pak Heri = 7 : 5. Sedangkan selisih uang mereka Rp 2.500.000. Maka besar uang pak heri adalah…
====================================
Hope Help Your Task!
#LearnWithBrainly
 Desain Grafis Indonesia Kumpulan Berita dan Informasi dari berbagai sumber yang terpercaya
Desain Grafis Indonesia Kumpulan Berita dan Informasi dari berbagai sumber yang terpercaya


