Lingkaran dengan ukuran panjang jari-jari 100 cm dan besar sudut pusat nya 90°. maka tentukan luas lingkaran dan luas juring lingkaran nya!
Mapel Matematika, Jenjang Sekolah Menengah Pertama
Jawaban:
Luas lingkaran:
L = πr²
L = 3,14 × 100²
L = 3,14 × (100×100)
L = 3,14 × 10.000
L = 31.400cm²
Luas juring:
Lj = a/360° × πr²
Lj = 90°/360° × 3,14 × 100²
Lj = 1/4 × 3,14 × (100×100)
Lj = 1/4 × 3,14 × 10.000
Lj = 1/4 × 31.400
Lj = 7.850cm²
Diketahui :
- Hari-hari lingkaran → 100 cm
- Sudut pusat lingkaran → 90°
Ditanya :
- Luas lingkaran…?
- Luas juring…?
Langkah-langkah :
- Luas lingkaran
- Luas juring
Jawaban~
✎ Luas lingkaran = 31.400 cm² ✔️
✎ Luas juring = 7.850 cm² ✔️
Pertanyaan Baru di Matematika
Jika rq=rs, buktikan bahwa segitiga pqr dan segitiga psr kongruen!
tolong bantu kak
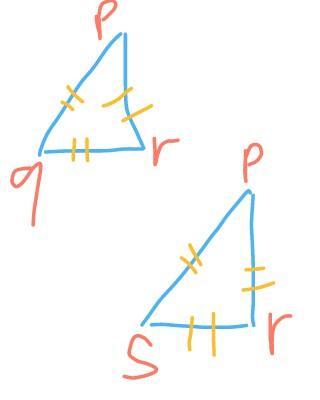
Matematika, Sekolah Menengah Atas
Penjelasan dengan langkah-langkah:
Jika misalkan panjang sisi RQ adalah 12 cm, maka panjang sisi RS juga sama.
Diketahui deret aritmatika : -1, 3, 7, …. jumlah 12 suku pertama barisan tersebut adalah

Matematika, Sekolah Menengah Pertama
Penjelasan dengan langkah-langkah:
jumlah 12 suku pertama nya adalah 252
cara terlampir yak
Q.
4b + 5a + 6b^a
a = 2
b = 3
Pake cara!

Matematika, Sekolah Menengah Atas
Penjelasan dengan langkah-langkah:
- 4b + 5a + 6b^a
- 4(3) + 5(2) + 6(3)²
- 12 + 10 + 6(9)
- 12 + 10 + 54
- 22 + 54
- 76
===========
Soal : Himpunan penyelesaian dari pertidaksamaan nilai mutlak |2x+2|>x-4 adalah?
soal rada sulit
peraturan sperti biasa
___jwbn yg grade 4 ato 5 DIJAMIN BeA:}
Matematika, Sekolah Menengah Pertama
|2x + 2| > x – 4
2x + 2 ≥ 0
2x ≥ 0 – 2
2x ≤ -2
x ≤ -2/2
x ≤ -1
2x + 2 < 0
2x < 0 – 2
2x < -2
x < -2
2x + 2 > x – 4
2x – x > -4 – 2
x < -6
-(2x + 2) > x – 4
-2x – 2 > x – 4
-2x – x > -4 + 2
-3x > -2
x < -2/-3
x > 2/3
Hp : x < –6 Atau x > 2/3
🙂
|2x+2|>x-4
2x + 2 ≥ 0
2x ≤ 2
2x + 2 < 0
2x < -2
x < – 2
2x + 2 > x – 4
2x – x > -4 – 2
x > -6
-2x + 2 > x – 4
-2x – 2 > -4 + 2
-3x > -2
x = 2/3
HP = { x < – 6 atau x = 2/3 }
4. Tentukan nilai lim x = π/2 cos x tan 2x / 2 sin x cos x 5. Tentukan nilai limit x= π/2 sin 5x + sin 3x / cos 5x + cos 3x
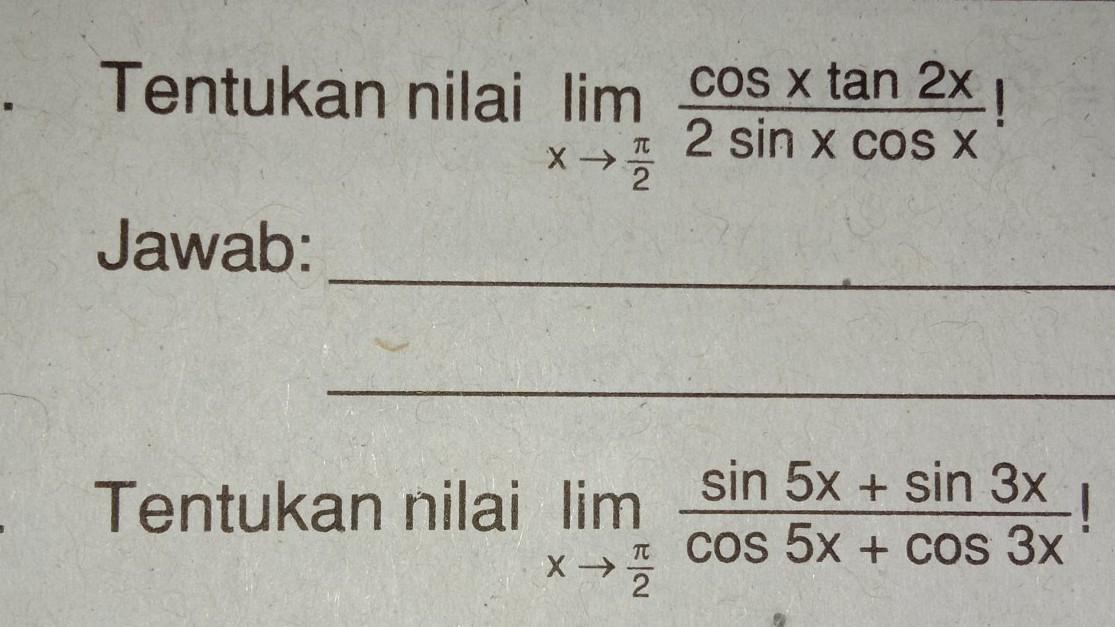
Matematika, Sekolah Menengah Atas
Penjelasan dengan langkah-langkah:
Nomor 4
Nomor 5
 Desain Grafis Indonesia Kumpulan Berita dan Informasi dari berbagai sumber yang terpercaya
Desain Grafis Indonesia Kumpulan Berita dan Informasi dari berbagai sumber yang terpercaya


