Himpunan penyelesaian dari pertidaksamaan nilai mutlak |2x+2|>x-4 Tolong banget pake penjelasannya dan garis bilangannya
Mapel Matematika, Jenjang Sekolah Menengah Pertama
Penjelasan dengan langkah-langkah:
|2x+2|>x-4
2x + 2 ≥ 0
2x ≤ 2
2x + 2 < 0
2x < -2
x < – 2
2x + 2 > x – 4
2x – x > -4 – 2
x > -6
-2x + 2 > x – 4
-2x – 2 > -4 + 2
-3x > -2
x = 2/3
HP = { x < – 6 atau x = 2/3 }
Jawaban:
Hp = {x < –6 atau x > ⅔}
Penjelasan dengan langkah-langkah:
|a| > x
Syarat 1
n > x
Syarat 2
n < -x
|2x + 2| > x – 4
- n > x
2x + 2 > x – 4
2x – x > -4 – 2
x > -6
- n < –x
2x + 2 < -(x – 4)
2x + 2 < -x + 4
2x + x < 4 – 2
3x < 2
x < 2/3
Pertanyaan Baru di Matematika
1. 57 x 29 = …..
2. 20 x 87=…….
jawab pake contoh nya

Matematika, Sekolah Dasar
1) 57 x 29 = 1653
2) 20 x 87 = 1740
– cara terlampir di atas –
579 x 45 = memakai cara
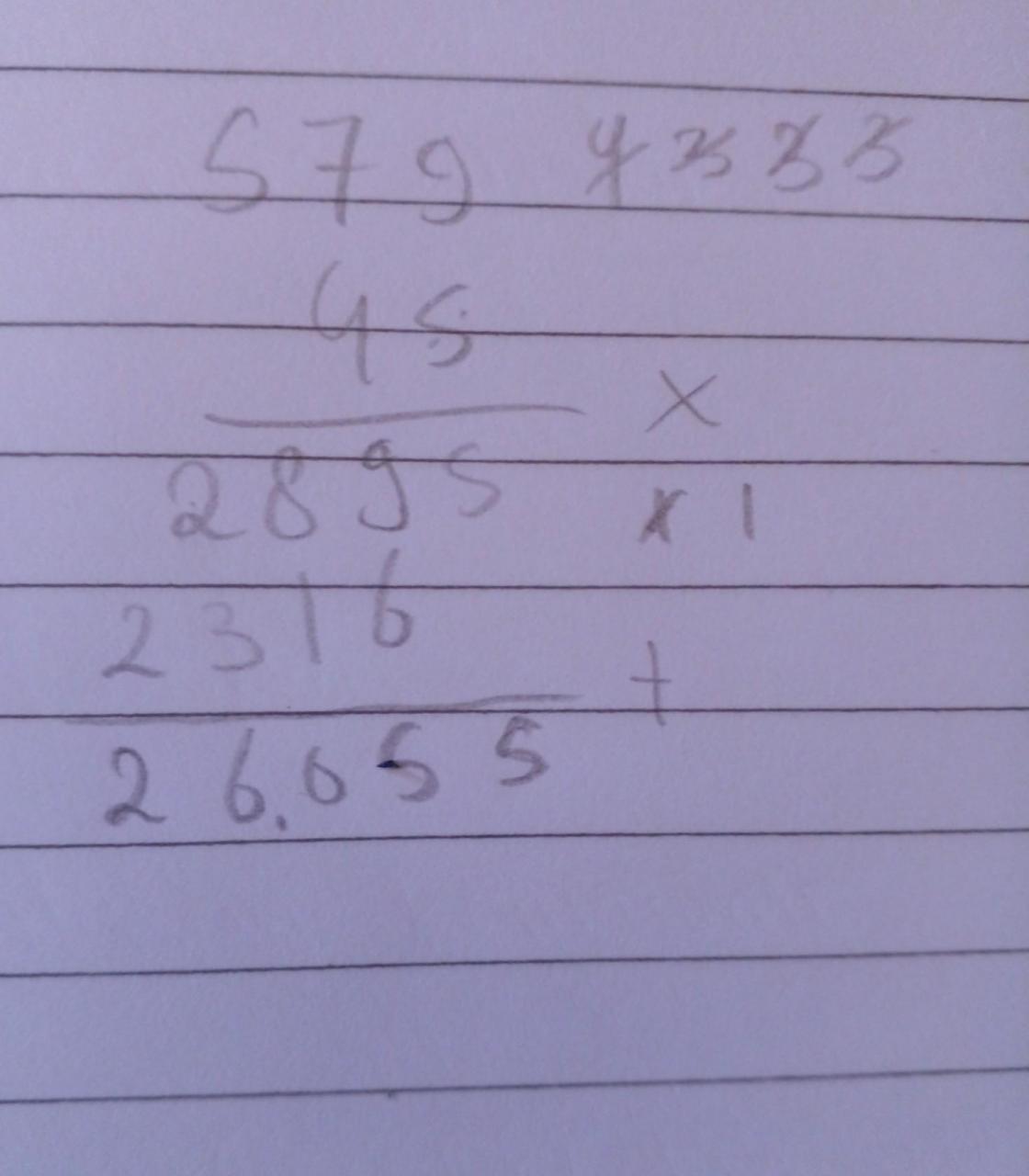
Matematika, Sekolah Menengah Pertama
Jawaban:
26.055
Penjelasan dengan langkah-langkah:
Sudah ada di foto silahkan di cek
579 × 45
Jawaban :
579 × 45
= 26.055
#SemogaMembantu
Semangat belajarnya ya!
Hasil dari ( 3x + 2 ) ( 2x – 5 )² adalah … A. 6x² + 19x – 10
B. 6x² – 19x – 10
C. 6x² – 11x – 10
D. 6x² – 11x + 10


Matematika, Sekolah Menengah Pertama
Jawaban:
- ( 3x + 2 ) ( 2x – 5 )² = tidak ada opsi
- ( 3x + 2 ) ( 2x – 5 ) = opsi C
Penjelasan dengan langkah-langkah:
Terlampir
Jadi, hasil dari (3x+2)(2x–5)² adalah 12x³–52x²+35x+50
A. nilai X
B. nilai sudut CBD

Matematika, Sekolah Menengah Pertama
Diketahui dua sudut dalam sepihak berjumlah 180°
A. 4x-4°+2x+7°=180°
6x+3°=180°
6x=180°-3°
6x=177°
x=29,5°
B. <CBQ
4x-4°
4(29,5)-4°
118°-4°
114°
<CBD+<CBQ=180°
<CBD+114°=180°
<CBD=180°-114°
<CBD=66°
Tolong dijawab,
jangan ngasal ,
buruan butuh banget nih !!!!!

Matematika, Sekolah Dasar
semoga membantu ya Jadikan jawaban terbaik
 Desain Grafis Indonesia Kumpulan Berita dan Informasi dari berbagai sumber yang terpercaya
Desain Grafis Indonesia Kumpulan Berita dan Informasi dari berbagai sumber yang terpercaya


