Tentukan 3 bilangan selanjutnya dari pola barisan bilangan 2,6,18,…,…,…

Tentukan 3 bilangan selanjutnya dari pola barisan bilangan 2,6,18,…,…,…

Mapel Matematika, Jenjang Sekolah Menengah Pertama

Pola barisan tersebut merupakan pola bilangan geometri. Maka 3 bilangan selanjutnya dari pola barisan bilangan 2, 6, 18 adalah 54, 162, 486.

Penjelasan dengan langkah-langkah

Untuk mencari 3 bilangan selanjutnya dari pola bilangan yang terdapat pada soal kita gunakan rumus barisan geometri du bawah ini.

Keterangan:

• Un = Suku ke n
• a = Suku awal
• r = Rasio
• n = Banyak suku

Barisan geometri merupakan barisan bilangan yang tersusun dengan rasio yang tetap.

Penyelesaian soal >>

Diketahui:

Barisan bilangan = 2, 6, 18

Ditanya:

Tiga bilangan selanjutnya...?

Jawab:

>> Langkah 1, kita tentukan rasio terlebih dahulu.

>> Langkah 2, kita cari tiga bilangan selanjutnya.

Suku ke 4

Suku ke 5

Suku ke 6

Kesimpulan:

Jadi, 3 bilangan selanjutnya dari pola bilangan tersebut adalah 54, 162, dan 486.

Pelajari lebih lanjut

• Materi tentang suku ke n =>
• Materi tentang barisan aritmatika =>
• Materi tentang barisan bilangan =>

===========================================================

Detail Jawaban

Kelas: IX SMP

Mapel: Matematika

Bab: Barisan dan Deret Bilangan

Kode: 9.2.2

#AyoBelajar #SPJ2

Pertanyaan Baru di Matematika

---

3a + 2 = a – 4
a = ?

​

Matematika, Sekolah Menengah Pertama

Penjelasan dengan langkah-langkah:

3a + 2 = a – 5

3a – a = – 4 – 2

3a – 1a = -6

2x = -6

x = -6/2

x = -3

Diketahui :

3a + 2 = a – 4

Ditanya :

Berapa nilai a?

Dijawab :

3a + 2 = a – 4

3a – a = – 4 – 2 (pindah ruas)

2a = -6

a = -6 ÷ 2

a = -3

Kesimpulan :

maka nilai a nya adalah –3.

---

Bantu jawab ya
#no ngasal jawab ​

Matematika, Sekolah Menengah Pertama

Jawaban:

1) membelah diri setiap 15 menit

60:15= 4 kali dalam 1 jam

4×24= 96 kali dalam 1 hari

4× 2^96

2) 1 jam =60 menit

4 kali

2^4=16

1000/16=62,5 atau 63 amoeba

KOREKSI JIKA SALAH

LIKE JIKA TERBANTU

1. Banyak amoeba S dalam 1 hari (terhitung setelah pengamatan dilakukan) adalah ekor, atau sama dengan ekor amoeba S.
2. Banyak amoeba S mula-mula sehingga dalam 1 jam terdapat minimal 1000 ekor amoeba S adalah ekor.

 

Pembahasan

Amoeba S membelah diri sebanyak 2 kali setiap 15 menit. Dengan asumsi pembelahan diri adalah dari 1 ekor menjadi 2 ekor, maka setelah dua kali membelah diri, 1 ekor amoeba S berkembang biak menjadi:
2×2 = 2² = 4 ekor.
Oleh karena itu, setiap 15 menit, 1 ekor amoeba S akan berkembang menjadi 4 ekor.

Jadi, kesimpulan sementara yang dapat diambil adalah rasio perkembangbiakan amoeba S dengan satuan durasi 15 menit adalah .

Soal a.

Dari suatu pengamatan diketahui ada 4 ekor amoeba S. Dengan satuan durasi 15 menit, untuk durasi 1 hari diperoleh:

Jadi, banyak amoeba S dalam 1 hari terhitung setelah pengamatan dilakukan adalah:
ekor amoeba S.

Kita juga dapat menghitung dengan barisan geometri. Perlu diperhatikan, bahwa dengan , bukan 96 melainkan 97, karena 4 ekor amoeba S adalah kondisi awal/inisial.

Banyak amoeba S dalam 1 hari terhitung setelah pengamatan dilakukan dinyatakan oleh , di mana , dengan . Akan diperoleh hasil yang sama, yaitu   atau sama dengan ekor amoeba S.

Soal b.

Dengan barisan geometri, adalah kondisi awal. adalah nilai yang ingin kita cari pada soal ini.

Menit ke-15: . Menit ke-30: . Dst. Sehingga menit ke-60 (satu jam): .

Oleh karena itu, banyak minimal amoeba S = 1000 ekor adalah nilai minimal dari . “Minimal” dapat diartikan sebagai “lebih dari atau sama dengan”.

Karena nilai harus merupakan bilangan bulat, maka pada perhitungannya akan melibatkan pembulatan jika kita cari nilai sebenarnya dari pecahan tersebut. Nilai terkecil yang lebih dari 125 adalah , dan selisih antara 128 dengan 125 adalah 3, cukup signifikan kurangnya dari . Maka, kita dapat mengganti 125 menjadi , dan pertidaksamaan menjadi persamaan.

∴  Jadi, banyak amoeba S mula-mula sehingga dalam 1 jam terdapat minimal 1000 ekor amoeba S adalah 4 ekor.

---

Isilah titik-titik dengan tanda “<” atau “>” agar menjadi kalimat yg benar!​

Matematika, Sekolah Dasar

Jawab:

Penjelasan dengan langkah-langkah:

Positif > Negatif , Angka Negatif Rendah > Angka negatif besar

jadi,

-5 < 4

0 < -3

-2 > -7

-3 < 6

---

Tolong di jawab ya terima kasih,tolong kerjakan yang kosong ya​

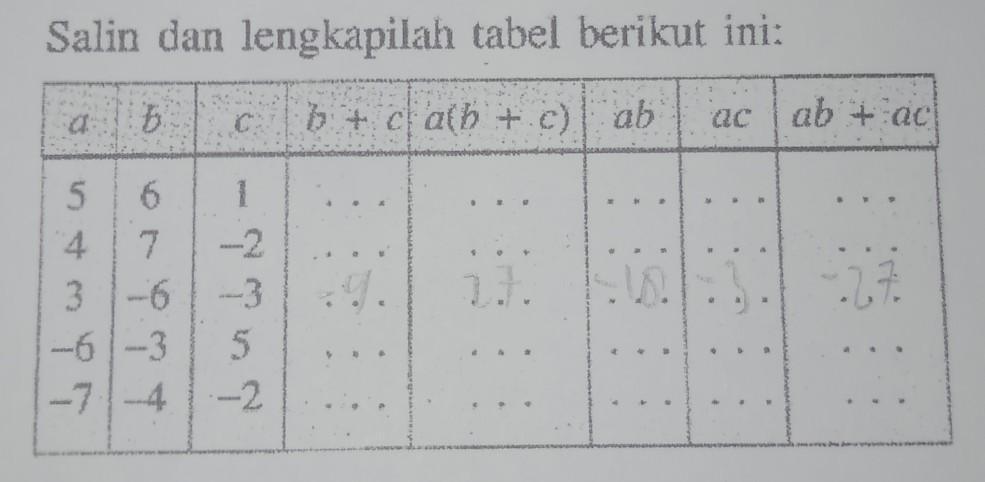
Matematika, Sekolah Menengah Atas

Jawab:

• 11, 35, 30, 5, 35
• 11, 20, 28, -8, 20
• -3, -27, -18, -9, -27
• -9, -12, 18, -30, -12
• -11, 42, 28, 14, 42

Penjelasan dengan langkah-langkah:

• 5+6=11 ; 5(6+1)=35 ; 5×6=30 ; 5×1=5 ; 30+5=35
• 4+7=11 ; 4(7+(-2))=20 ; 4×7=28 ; 4x(-2)=-8 ; 28+(-8)=20
• 3+(-6)=(-3) ; 3(-6+(-3))=(-27) ; 3x(-6)=(-18) ; 3x(-3)=(-9) ; -18+(-9)=(-27)
• -6+(-3)=(-9) ; -6(-3+5)=(-12) ; -6x(-3)=18 ; -6×5=(-30) ; 18+(-30)=(-12)
• -7+(-4)=-11 ; -7(-4+(-2))=42 ; -7x(-4)=28 ; -7x(-2)=14 ; 28+14=42

(+) x (+) = (+)

(+) x (-) = (-)

(-) x (-) = (+)

(-) x (+) = (-)

---

Kerjakan pembagian pecahan di bawah ini 2. 8/20:2/2= 3. 14/12:2/2= 4. 21/4:3/3= 5. 21/4:3/3=​

Matematika, Sekolah Dasar

Jawab:

Penjelasan dengan langkah-langkah:

2. 8/20 : 2/2
Dikecilin dan kalau bagi dibalik + jadi perkalian:

2/5 x 1 = 2/5

3. 14/12 : 12/2

7/6 x 1/6 = 7/36

4. 21/4 : 3/3

21/4 x 1 = 21/4

5. Sama kayak no. 4