Buktikan dengan induksi matematika : 2 + 7 + 12 + 17 + …. + (5n – 3) = (5n² – n / 2)! Note: Sepertinya hati saya ini kembali terbuka karena seseorang tapi saya gak bakalan sebutin siapa seseorang yang buat hati saya kembali terbuka

Q. Buktikan dengan induksi matematika :
2 + 7 + 12 + 17 + …. + (5n – 3) = (5n² – n / 2)!

Note: Sepertinya hati saya ini kembali terbuka karena seseorang tapi saya gak bakalan sebutin siapa seseorang yang buat hati saya kembali terbuka​

Mapel Matematika, Jenjang Sekolah Menengah Atas

Terbukti benar bahwa

untuk setiap bilangan asli.
___________________

Pembahasan

Pada pembuktian dengan induksi matematika, terdapat 3 langkah, yaitu:

• Langkah pertama: Basis Induksi
  Pada langkah ini, kita membuktikan bahwa pernyataan matematika benar untuk (nilai terkecil pada bilangan asli). Pada induksi matematika yang diperluas, nilai basis ini tidak harus sama dengan 1, tergantung pada himpunan bilangan di mana pernyataan matematika tersebut berlaku.
• Langkah kedua: Asumsi (hipotesis)
  Pada langkah ini, kita menetapkan asumsi/hipotesis, bahwa pernyataan matematika yang ingin dibuktikan benar berlaku untuk sembarang nilai bilangan asli, atau pada himpunan bilangan di mana pernyataan matematika tersebut berlaku. Oleh karena itu, pada langkah ini diambil .
• Langkah ketiga: Langkah Induksi
  Pada langkah ini, dengan cara tertentu, harus dapat dibuktikan bahwa pernyataan matematika tersebut berlaku untuk .

Jika langkah induksi terbukti, maka hal tersebut membuktikan asumsi/hipotesis berlaku.

Persoalan

Kita akan membuktikan

untuk setiap bilangan asli.

PEMBUKTIAN dengan Induksi Matematika

Selanjutnya, kita sebut deret sebagai .

Basis Induksi
Untuk , terbukti benar bahwa .

Asumsi (Hipotesis)

Andaikan benar untuk , yaitu

Langkah Induksi

Harus ditunjukkan/dibuktikan bahwa

KESIMPULAN

Telah ditunjukkan bahwa langkah induksi untuk terbukti benar.
∴  Dengan demikian, terbukti bahwa

berlaku untuk setiap bilangan asli.

___________________

Pelajari Lebih Lanjut

Contoh soal lain tentang Induksi Matematika

___________________

Detail Jawaban

Mata Pelajaran: Matematika
Kelas: 11 (XI)
Materi: Bab 1 – Induksi Matematika
Kode Kategorisasi: 11.2.1

Pertanyaan Baru di Matematika

---

755.862 dalam bentuk Huruf bilangan ratusan ribuan puluhan
​

Matematika, Sekolah Menengah Atas

Jawaban:

Tujuh ratus lima puluh lima ribu, delapan ratus enam puluh dua.

Penjelasan dengan langkah-langkah:

Semoga bermanfaat

Penyelesaian

Dalam bentuk Angka : 755.862

__________&____________

Dalam bentuk huruf :

Tujuh Ratus lima puluh lima ribu delapan ratus enam puluh dua

---

-472 -230 + 428 =
tolong cuk udh tau jawabannya tpi takut salah​

Matematika, Sekolah Menengah Atas

– Penyelesaian Soal –

Penyelesaian dan Hasil :

i Hope This Help-!

---

Quis. 1.) 546 + 235 =
2.) 452 – 321 =
3.) 651 × 53 =

nt : menggunakan cara bersusun ​

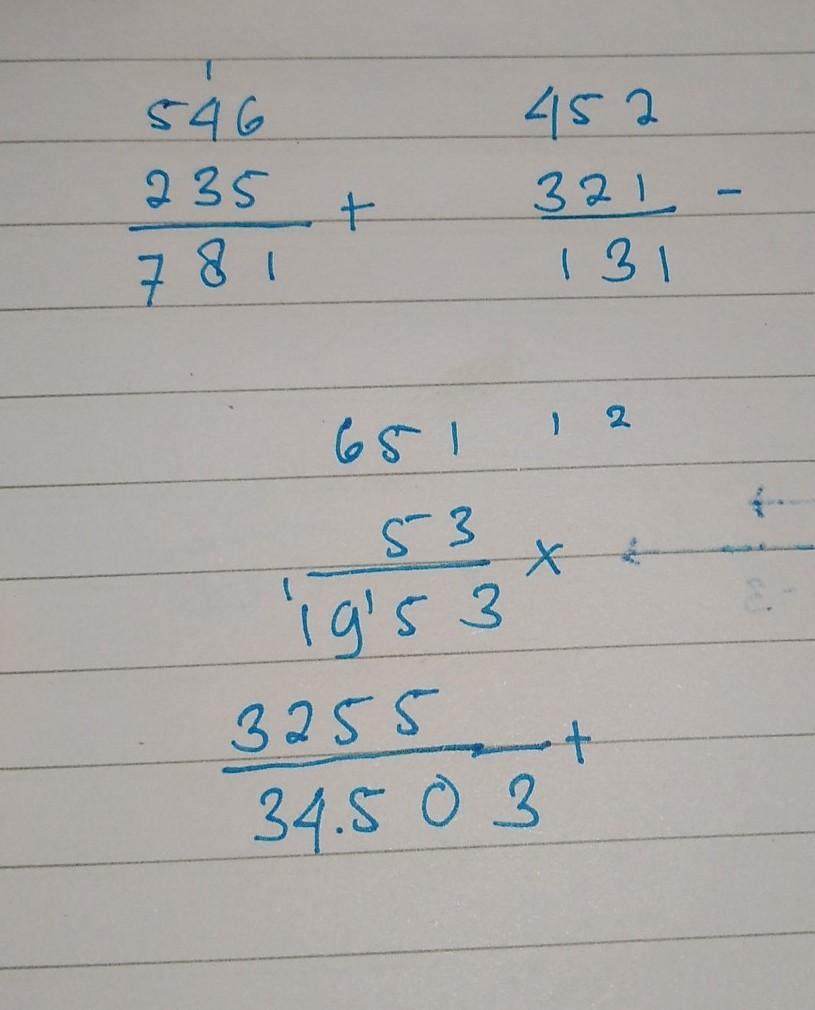
Matematika, Sekolah Menengah Pertama

1) 546 + 235 = 781

2) 452 – 321 = 131

3) 651 × 53 = 34.503

– Penyelesaian Soal –

[ 1 ]

546 + 235 = ?

• 546 + 235
• = 781 ☑

[ 2 ]

452 – 321 = ?

• 452 – 321
• = 131 ☑

[ 3 ]

651 × 53 = ?

• 651 × 53
• = 34.503 ☑

Kesimpulan

• Hasil 1 = 781 ✔️
• Hasil 2 = 131 ✔️
• Hasil 3 = 34.503 ✔️

i Hope This Help

---

Tentukan 3 bilangan selanjutnya dari pola barisan bilangan 2,6,18,…,…,…

Matematika, Sekolah Menengah Pertama

Pola barisan tersebut merupakan pola bilangan geometri. Maka 3 bilangan selanjutnya dari pola barisan bilangan 2, 6, 18 adalah 54, 162, 486.

Penjelasan dengan langkah-langkah

Untuk mencari 3 bilangan selanjutnya dari pola bilangan yang terdapat pada soal kita gunakan rumus barisan geometri du bawah ini.

Keterangan:

• Un = Suku ke n
• a = Suku awal
• r = Rasio
• n = Banyak suku

Barisan geometri merupakan barisan bilangan yang tersusun dengan rasio yang tetap.

Penyelesaian soal >>

Diketahui:

Barisan bilangan = 2, 6, 18

Ditanya:

Tiga bilangan selanjutnya...?

Jawab:

>> Langkah 1, kita tentukan rasio terlebih dahulu.

>> Langkah 2, kita cari tiga bilangan selanjutnya.

Suku ke 4

Suku ke 5

Suku ke 6

Kesimpulan:

Jadi, 3 bilangan selanjutnya dari pola bilangan tersebut adalah 54, 162, dan 486.

Pelajari lebih lanjut

• Materi tentang suku ke n =>
• Materi tentang barisan aritmatika =>
• Materi tentang barisan bilangan =>

===========================================================

Detail Jawaban

Kelas: IX SMP

Mapel: Matematika

Bab: Barisan dan Deret Bilangan

Kode: 9.2.2

#AyoBelajar #SPJ2

---

Bantu kak(╯︵╰,)
semoga yang bantu in aku rezekinya makin banyak aminnn…..​

Matematika, Sekolah Dasar

Jawaban:

Jadi caranya gini

IPA+IPS-YANG SUKA KEDUANYA

28+15-6=37

39 – 37 = 2 (A)

Penjelasan dengan langkah-langkah:

SEMOGA MEMBANTU

JADIKAN JAWABAN TERBAIK YA:)