Soal :
7!! × 4!
77 – 44 + 22
5!
otw hapus.
Mapel Matematika, Jenjang Sekolah Menengah Pertama
7!! × 4!
( 7 × 5 × 3 × 1 ) × ( 4 × 3 × 2 × 1 )
( 35 × 3 ) × ( 12 × 2 )
105 × 24
1.520
–––––––––––––––––––––––––––––––––––
77 – 44 + 22
33 + 22
55
–––––––––––––––––––––––––––––––––––
5!!
5 × 4 × 3 × 2 × 1
20 × 3 × 2
60 × 2
120
#BelajarBersamaBrainly
PEMBAHASAN :
Diketahui :
1. 7!! × 4!
2. 77 – 44 + 22
3. 5!
Ditanya :
hasilnya adalah?
Jawaban :
nomor satu
= 7!! × 4!
= ( 7 × 5 × 3 × 1 ) × 4!
= ( 35 × 3 × 1 ) × 4!
= ( 105 × 1 ) × 4!
= 105 × 4!
= 105 × ( 4 × 3 × 2 × 1 )
= 105 × ( 12 × 2 × 1 )
= 105 × ( 24 × 1 )
= 105 × 24
= 2.520
============
nomor dua
= 77 – 44 + 22
= 33 + 22
= 55
============
nomor tiga
= 5!
= 5 × 4 × 3 × 2 × 1
= 20 × 3 × 2 × 1
= 60 × 2 × 1
= 120 × 1
= 120
Pertanyaan Baru di Matematika
 beri dengan penjelasan cara
beri dengan penjelasan cara
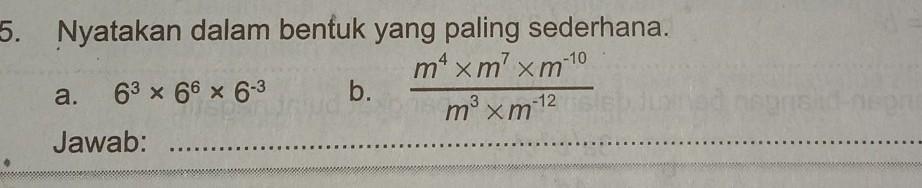
Matematika, Sekolah Menengah Atas
Jawab:
5a. = 6⁶
5b. = m¹⁰
Penjelasan:
Aturan perkalian atau
pembagian eksponen:
aᵇ×aᵇ = aᵇ⁺ᵇ
aᵇ×a⁻ᵇ = aᵇ÷aᵇ = aᵇ⁻ᵇ
5a.
6³×6⁶×6⁻³ = (6³×6⁻³)×6⁶
= (6³⁻³)×6⁶ = 6⁰×6⁶
= 6⁰⁺⁶
= 6⁶
5b.
(m⁴×m⁷×m⁻¹⁰)÷(m³×m⁻¹²) =
m⁴÷(m³×m⁻¹²) × (m⁷×m⁻¹⁰) =
(m⁴÷m³) × m¹²×m⁷×m⁻¹⁰ =
(m⁴⁻³) × m¹²⁺⁷⁻¹⁰ =
m¹ × m⁹ =
m¹⁺⁹
= m¹⁰
(xcvi)
Penjelasan dengan langkah-langkah:
Bagian A.
6³ × 6⁶ ×
dengan menggunakan sifat eksponen!
———–
Bagian B.
Tolong Jawab dengan cara nya soal ada di gambar
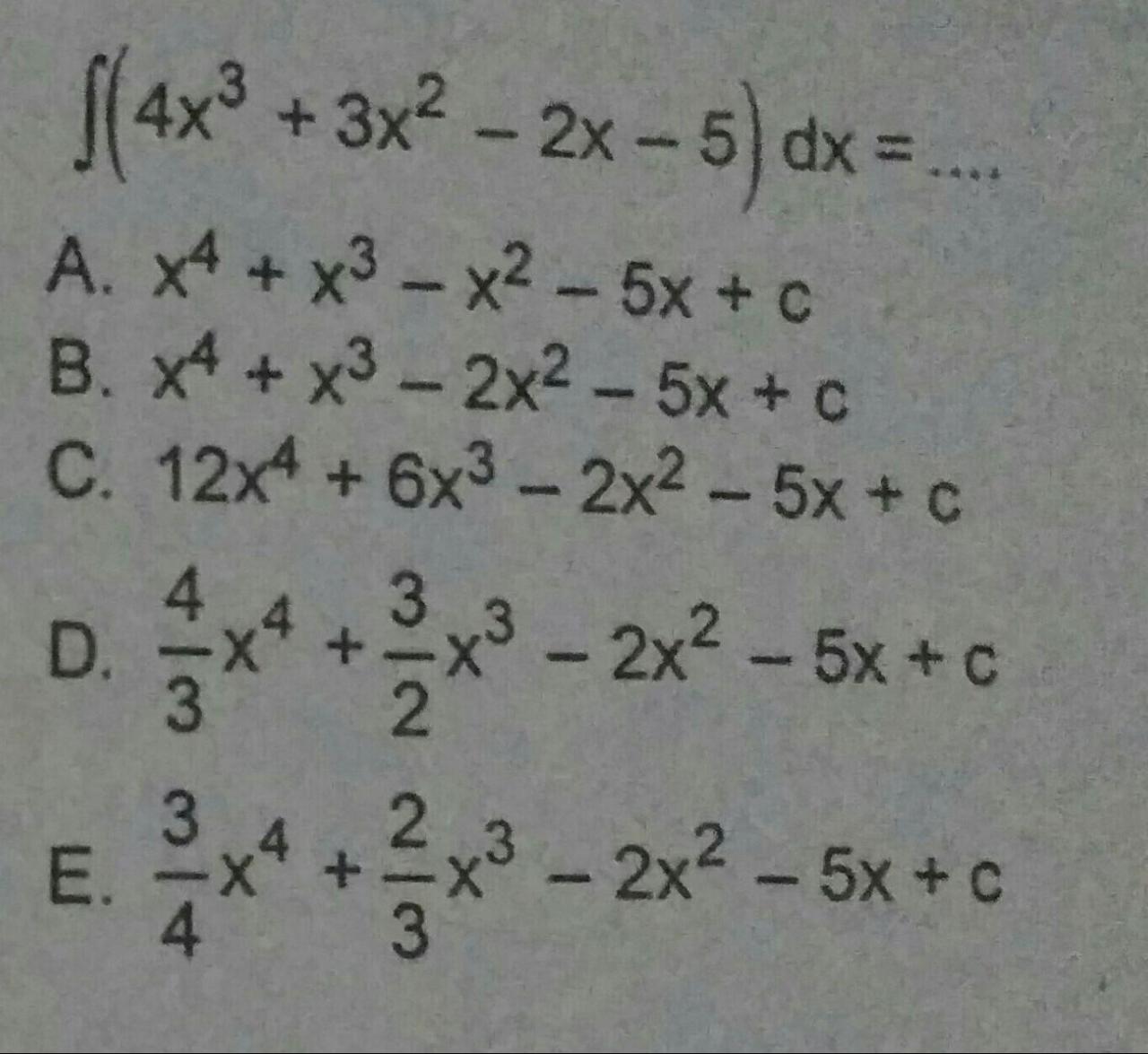
Matematika, Sekolah Menengah Atas
Jawab:
Kuis: super mudah, yang duluan dpt BA Carilah nilai p dari persamaan-persamaan berikut ini.
(a.) 4p = 16
(b.) 1 + 1 = p – 1
(c.) p² – 4 = 0
(d.) 3p² = 48
(e.) p + p + p + p + p = 5
Matematika, Sekolah Menengah Atas
Jawab:
(a.) p = 4
(b.) 3 = p
(c.) p = 2
(d.) p = 4
(e.) p = 1
Penjelasan dengan langkah-langkah:
(a.) 4p = 16
Untuk mendapatkan nilai p dari persamaan ini, kita kalikan kedua ruas kanan dan kiri dengan 1/4, maka:
4p x 1/4 = 16 x 1/4 kita dapatkan hasil p:
p = 4
(b.) 1 + 1 = p – 1
Untuk mendapatkan nilai p dari persamaan ini, kita pindahkan angka -1 ke ruas kiri, menjadi:
1 + 1 = p – 1
2 = p – 1
2 + 1 = p
3 = p
(c.) p² – 4 = 0
Untuk mendapatkan nilai p dari persamaan ini, kita tambahkan kedua ruas dengan angka 4, kemudian hasilnya kita dapatkan akar dari angka perpindahan ruas tersebut:
p² – 4 = 0
p² = 4
p =
p = 2
(d.) 3p² = 48
Untuk mendapatkan nilai p dari persamaan ini, kita kalikan kedua ruas dengan 1/3, maka:
3p² x 1/3 = 48 x 1/3
p² = 16
p =
p = 4
(e.) p + p + p + p + p = 5
Untuk mendapatkan nilai p dari persamaan ini, kita jumlahkan semua p yang berada di ruas kiri, lalu kita kalikan kedua ruas dengan 1/5, maka akan kita dapatkanlah nilai p:
p + p + p + p + p = 5
5p = 5 lalu kita kalikan kedua ruas dengan 1/5:
5p x 1/5 = 5 x 1/5
p = 1
Semoga membantu ya.
3 1/4 kg – 1.75 kg + 2 1/2 kg = ?
Matematika, Sekolah Menengah Pertama
Jawaban:
3¼ kg – 1,75 kg + 2 ½ kg = 4kg
Penjelasan dengan langkah-langkah:
Jawaban:
4 kg
Penjelasan dengan langkah-langkah:
3 1/4 kg – 1,75 kg + 2 1/2 kg = ?
(Ubah dahulu semuanya menjadi pecahan)
13/4 kg – 175/100 kg + 5/2 kg = ?
(Samakan semua penyebut nya terlebih dahulu)
325/100 – 175/100 + 250/100 =
150/100 + 250/100 = 400/100
= 4 kg
Pak Budiman berangkat dari Banjarmasin ke Amuntai mengendarai mobil pada adalah 200 km. Dalam perjalanan, Pak Budiman istirahat selama 30 menit. Pada pukul 07.00 dengan kecepatan rata-rata 50 km/jam. Jarak kedua kota tersebut pukul berapa Pak Budiman akan tiba di Amuntai?
Matematika, Sekolah Dasar
Jawaban :
Rumus :
Waktu (t) = Jarak (s) ÷ Kecepatan (v)
t = s/v
t = 200/50
t = 4
Jam 07:00 + 04:00 (perjalanan) + 00:30 (istirahat) = 11:30
 Desain Grafis Indonesia Kumpulan Berita dan Informasi dari berbagai sumber yang terpercaya
Desain Grafis Indonesia Kumpulan Berita dan Informasi dari berbagai sumber yang terpercaya


