[4/10] f(x) = 3x – 2 g(x) = 4x + 1 f(1) + g(1) = …

[4/10]
f(x) = 3x – 2
g(x) = 4x + 1

f(1) + g(1) = …​

Mapel Matematika, Jenjang Sekolah Menengah Atas

Penjelasan dengan langkah-langkah:

= f(1) + g(1)

= 3(1) – 2 + 4(1) + 1

= 3 – 2 + 4 + 1

= 1 + 5

= 6

f(x) = 3x – 2

g(x) = 4x + 1

f(1) + g(1)

= [3(1) – 2] + [4(1) + 1]

= [3 – 2] + [4 + 1]

= 1 + 5

= 6

Pertanyaan Baru di Matematika

---

F(x) = x³ – 2x¹ × 6!!!
f(3) = …………………..
@Brainlymoderat TvT​

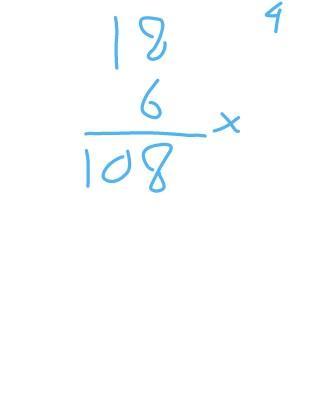
Matematika, Sekolah Menengah Pertama

f(x) = x³ – 2x¹ × 6!!!

f(3) = 3³ – 2(3¹) × 6!!!

f(3) = 3(3.3) – 2(3) × 6(3)

f(3) = 9(3) – 2(3) × 6(3)

f(3) = 27 – 6 × 18

f(3) = 27 – 108

f(3) = –81

🙂

Penjelasan dengan langkah-langkah:

f(x) = x³ – 2x¹ × 6!!!

f(3) = 3³ – 2(3¹) × 6!!!

f(3) = ( 3×3×3 ) – ( 2×3 ) × ( 6×3 )

f(3) = ( 9×3 ) – 6 × 18

f(3) = 27 – 6 × 18

f(3) = 27 – ( 6×18 )

f(3) = 27 – 108

f(3) = –81 ✅

___________________________

🙂

#BelajarBersamaBrainly

---

17.056: V 144 = ….
A. 16
B. 12
C. 10
D. 7​

Matematika, Sekolah Dasar

Mungkin “V” adalah “√”

=√144

=√12²

=12

Jadi, jawabannya adalah 12

Jawaban:

Hasil Dari √144 adalah B. 12

Pendahuluan:

Akar dalam matematika adalah suatu penyelesaian dari pembagian yang dibentuk menjadi suatu nilai akar.

Contohnya:

• √1 = 1
• √100 = 10
• √9 = 3
• √4 = 2
• √25 = 5

Rumus Akar:

Sebenarnya akar tidak memiliki rumus, tetapi Akar terbentuk karena adanya Hasil dari pembagian yang bisa dibagi dan dibentuk menjadi bentuk akar.

Penyelesaian Soal:

Mungkin “V” Adalah “√”

√144

= √144 ÷ 12

= √12

= 12

Kesimpulan:

Hasil dari √144 adalah B. 12

---

Hai selamat sore:^
jwb pertnyaan brikut!

soal:
Sebuah balok berukuran panjang 14 cm lebar 4 cm dan tinggi 2 cm, maka tentukan Luas permukaannya

jwb dgn menggunakan cara ✅
jgn ngasal ✅​

Matematika, Sekolah Menengah Pertama

Jawaban:

Luas permukaan Balok tersebut adalah 184 cm²

Pendahuluan:

Balok adalah suatu bangun ruang yang memiliki sisi yang berbentuk seperti gabungan dari ruang bangun persegi dan persegi panjang. Balok memiliki 12 rusuk, 6 sisi, dan 8 titik sudut.

Rumus Balok:

• Luas Permukaan:

Lp = 2(pl + pt + lt)

Lp = 2pl + 2pt + 2lt

• Volume:

V = p × l × t

• Keliling:

K = 4 × (p + l + t)

Penyelesaian:

Cara 1:

Lp = 2(pl + pt + lt)

Lp = 2((14×4) + (14×2) + (4×2))

Lp = 2(56 + 28 + 8)

Lp = 2(84 + 8)

Lp = 2(92)

Lp = 2 × 92

Lp = 184 cm²

Cara 2:

Lp = 2pl + 2pt + 2lt

Lp = 2(14×4) + 2(14×2) + 2(4×2)

Lp = 2(56) + 2(28) + 2(8)

Lp = 112 + 56 + 16

Lp = 168 + 16

Lp = 184 cm²

Kesimpulan:

Luas permukaan Balok tersebut adalah 184 cm²

Sebuah balok berukuran panjang 14 cm lebar 4 cm dan tinggi 2 cm, maka tentukan Luas permukaannya!

Langkah – Langkah mengerjakan :

P = 14 cm

L = 4 cm

T = 2 cm

Luas permukaan :

= 2 × (p × l) + 2 × (p × t) + 2 × (l × t)

= 2 × (14 × 4) + 2 × (14 × 2) + 2 × (4 × 2)

= 122 + 56 + 16

= 194 cm^2

Jadi, ruas permukaan balok tersebut adalah 194 cm^2

---

[4/10]
f(x) = 3x – 2
g(x) = 4x + 1

f(1) + g(1) = …​

Matematika, Sekolah Menengah Atas

Penjelasan dengan langkah-langkah:

= f(1) + g(1)

= 3(1) – 2 + 4(1) + 1

= 3 – 2 + 4 + 1

= 1 + 5

= 6

f(x) = 3x – 2

g(x) = 4x + 1

f(1) + g(1)

= [3(1) – 2] + [4(1) + 1]

= [3 – 2] + [4 + 1]

= 1 + 5

= 6

---

Q:) 1 + 1 :v aku
Panjang diameter alas sebuah kerucut adalah 42 cm dan tingginya 40 cm. Volume kerucut tersebut adalah …
a. 18.480 cm³
b. 27.720 cm³
c. 41.580 cm³
d. 55.440 cm³
e. Tidak ada di opsi


≈ Sertakan cara penyelesaian!
≈ ngasal → report!
≈ Rapi!
≈ Salah → koreksi!
≈ grade 3/5 dijamin beA!

​

Matematika, Sekolah Menengah Pertama

V = ⅓ × La × Tl

V = ⅓ × 22/7 × 21² × 40

V = ⅓ × 22/7 × 441 × 40

V = ⅓ × 22/7 × 17.640

V = ⅓ × 55.440

V = 18.480 cm³ [ A. ]

🙂

Panjang diameter alas sebuah kerucut adalah 42 cm dan tingginya 40 cm. Volume kerucut tersebut adalah 18.480 cm³.

Pendahuluan

Bangun ruang kerucut adalah bangun ruang yang terdiri dari sisi lengkung dan alas yang berbentuk lingkaran. Kerucut di definisikan sebagai bangun ruang yang menyerupai limas segi (n).

Bangun ruang kerucut mempunyai beberapa ciri-ciri. Berikut adalah ciri-ciri dari bangun ruang kerucut!

Ciri – ciri kerucut

1. Memiliki 2 sisi yang berbentuk lingkaran
2. 1 sisi alas yang berbentuk lingkaran dan 1 nya lagi adalah sisi lengkung.
3. Hanya memiliki 1 rusuk.
4. Mempunyai selimut permukaan.
5. Memiliki 1 titik sudut.

Nah, selanjutnya, adalah rumus – rumus bangun ruang Kerucut! Catat yawh :D.

• – – – – • – – – – • – – – – •

Volume Kerucut

atau,

—

Luas Permukaan Kerucut

atau,

.

—

Luas Selimut Kerucut

Keterangan :

v = volume

r = jari – jari

s = panjang sisi miring

t = tinggi

= 3,14 atau ²²/7

======================================

Sekarang langsung saja selesaikan soalnya! :)

Pembahasan

Diketahui :

panjang diameter alas 42 cm dan tinggi 40 cm.

• – – – – • – – – – • – – – – •

Ditanya :

Volume kerucut?

• – – – – • – – – – • – – – – •

Jawab :

v = ⅓ × ²²/7 × (42 ÷ 2) cm² × 40 cm

v = ⅓ × ²²/7 × 21 cm² × 40 cm

v = ⅓ × ²²/7 × 441 cm × 40 cm

v = ⅓ × ²²/7 × 17.640 cm

v = ⅓ × 55.440 cm²

v =

• – – – – • – – – – • – – – – •

Kesimpulan

Jadi, volume kerucut nya 18.480 cm³.

• – – – – • – – – – • – – – – •

╭┈─────── ೄ࿐

╰┈─➤ Learn More :

Rumus bangun ruang kerucut

Contoh soal mengenai bangun ruang kerucut

Pengertian kerucut dan rumusnya

=======================================

∂єтαιℓ נαωαвαη ꕤ ─ ✉

• Mapel : Matematika
• Kelas : 4
• Materi : Bab 8 – Bangun datar dan bangun ruang.
• Kode Mapel : 2
• Kode Kategori : 4.2.8

Kata Kunci : Bangun ruang kerucut.

======================================

#BelajarBersamaBrainly