❤Soal math❤ 5 poin je

Matematika Comments Off on ❤Soal math❤ 5 poin je 47 Views

❤Soal math❤ 5 poin je Apa yang dimaksud Perpangkatan Eksponen? Jelaskan beserta contohnya!

Catatan :
Selamat mengerjakann ^_^

#JomBelajar

Mapel Matematika, Jenjang Sekolah Menengah Pertama

Pendahuluan

atau bisa di sebut Eksponen adalah bilangan yang di kalikan dengan bilangan tersebut. Bilangan berpangkat di kalikan sesuai pangkat nya Tersebut. Bentuk umum bilangan berpangkat di nyatakan sebagai aⁿ (di baca a pangkat n), di mana a di kalikan sebanyak (n).

Sifat-sifat Bilangan Berpangkat (Eksponen)

Keterangan :

aⁿ = a × a × a × …

n = eksponen atau pangkat

a = bilangan pokok atau basis

aⁿ = bilangan berpangkat atau eksponen

a × a × a × … sampai dengan n suku merupakan hasil perpangkatan

Contoh soal

Jadi Hasil Dari 5⁵ Adalah 3.125

Detail Jawaban

Mapel : Matematika
Kelas : 9 (SMP)
Bab : 1
Materi : Bilangan Berpangkat
Kata Kunci : Bilangan Berpangkat, Eksponen,Contoh soal
Kode Soal : 2
Kode Kategorisasi :

— ‹ Pendahuluan

Perpangkatan Atau Bisa Jugaa Disebut Dengan Eksponen adalah suatu bentuk perkalian dengan bilangan yang sama kemudian di ulang-ulang, semacam perkalian yang diulang-ulang. perpangkatan ialah perkalian yg berulang ulang dari faktor faktor bilangan yg sama sesuai pangkatnya. perpangkatan juga memiliki sifat – sifat eksponen ada beberapa macam eksponen di matematika diantaranya yaitu :

➳ Bilangan Eksponen Terdiri

— Bilangan Berpangkat Positif

➳ Bilangan Berpangkat Positif Merupakan Suatu Bilangan Yang Mempunyai Sifat Pangkat Atau Eksponen Yang Bersifat Positif .

— Bilangan Berpangkat Negatif

➳ Bilangan Berpangkat Negatif Adalah Suatu bilangen berpangkat negatif yang merupakan bilangan yang mempunyai pangkat atau eksponen nya tersebut.

— Bilangan Berpangkat Nol

➳ Bilangan Berpangkat Nol Adalah Suatu Bilangan jika pada bentuk tersebut nilai m sama dengan nilai n Maka akan m – n = 0 dipangkatkan nol itu pasti hasilnya satu kalau dijabarkan jika dikurangi hasilnya tetap nol.

— Bilangan Berpangkat Dalam Bentuk Akar

➳ Bilangan Berpangkat Dalam Bentuk Akar Adalah suatu tanda “√”, atau biasa juga disebut sebagai tanda akar Untuk menyederhanakan akar kuadrat, kita hanya harus memfaktorkan angkanya dan menarik akar kuadrat dari kuadrat sempurna.

______________________

❝ Contoh Bilangan Pangkat 2

1² = 1 × 1 = 1
2² = 2 × 2 = 4
3² = 3 × 3 = 9
4² = 4 × 4 = 16
5² = 5 × 5 = 25
6² = 6 × 6 = 36
7² = 7 × 7 = 49
8² = 8 × 8 = 64
9² = 9 × 9 = 81
10² = 10 × 10 = 100

______________________

❝ Contoh Bilangan Pangkat 3

1³ = 1 × 1 × 1 = 1
2³ = 2 × 2 × 2 = 8
3³ = 3 × 3 × 3 = 27
4³ = 4 × 4 × 4 = 64
5³ = 5 × 5 × 5 = 125
6³ = 6 × 6 × 6 = 216
7³ = 7 × 7 × 7 = 343
8³ = 8 × 8 × 8 = 512
9³ = 9 × 9 × 9 = 729
10³ = 10 × 10 × 10 = 1.000

______________________

❝ Sifat – Sifat Eksponen ‹

❝ Keterangan :

a & b ➳ Bilangan pokok / basis
m & n ➳ Pangkat / eksponen

Pembahasan-! ꒰⑅꒱

10² + 5² = ?

= ( 10 × 10 ) + ( 5 × 5 )

= 100 + 25

= 125

– ᴋᴇsɪᴍᴘᴜʟᴀɴ:

Jadi hasil dari 10² + 5² = ? adalah 125

______________________

— Pelajari Lebih Lanjut :

➳ Apa itu bilangan berpangkat?

➳ Perpangkatan, bentuk akar :

➳ Perkalian pecahan berpangkat :

➳ apa arti dari perpangkatan

➳ 10 sifat-sifat perpangkatan beserta contohnya

➳ Pengertian Perpangkatan :

— Detail Jawaban:

➳ Mapel : Matematika
➳ Kelas : IX SMP
➳ Materi : Bab 1 – Perpangkatan
➳ Kode soal : 2
➳ Kode Kategorisasi : 9.2.1
➳ Kata kunci : Cara Menghitung Perpangkatan 10 Sifat Sifat Perpangkatan Pengertian Perpangkatan, Perkalian Pecahan Berpangkat , Perpangkatan Dalam Bentuk sederhana

Pertanyaan Baru di Matematika

Q. 146 – (-12) =

(-23) + (-20) =

“Sebenarnya yg hrs bil Terimakasih itu..kita atau penjual ny?,, klo kita bil mksh..kenapwa yg jualan ikut bil teyimakasih?” :v

Matematika, Sekolah Dasar

Jawaban:

∆Pembahasan∆

Bilangan Bulat adalah Bilangan Yang terdiri dari bilangan bulat Positif , bilangan negatif, dan

Bilangan Nol

Operasi Hitung

Pertambahan

Pengurangan

Jawaban:

➣Nomor 1:

Hasil pengurangan bilanagan bulat dari 146-{-12} adalah 158

➣Nomor 2:

Hasil penjumlahan bilanagan bulat dari {-23}+{-20} adalah -43

✰▬▬▬▬▬▬▬※☠※▬▬▬▬▬▬▬✰

Pendahuluan:

Bilangan bulat merupakan sebuah bilangan yang dibagi menjadi 2 jenis yaitu bilangan bulat positif “+” dan juga bilangan negatif “-“.

✎Misalnya:

=5+{-3}

=5-3

✰▬▬▬▬▬▬▬※☠※▬▬▬▬▬▬▬✰

Pembahasan:

➣Nomor 1:

=146-{-12}

=146+12

=158

➣Nomor 2:

={-23}+{-20}

=23+20

=43

=-43

✰▬▬▬▬▬▬▬※☠※▬▬▬▬▬▬▬✰

Detail:

Mapel:Matematika

Kelas:VI – 6

Tingkat:SD – Sekolah Dasar

Materi:Bab 1 – Operasi hitung bulat

Kata kunci:Bilangan negatif,Perkalian,Penjumlahan,Pengurangan

Kode soal:2

Kode:6.2.1

✰▬▬▬▬▬▬▬※☠※▬▬▬▬▬▬▬✰

#BelajarBersamaBrainly

#AyoBelajar

#TingkatkanPrestasimu

#BelajarDenganMiracle

Kuis: super mudah, yang duluan dpt BA Carilah nilai p dari persamaan-persamaan berikut ini.

(a.) 4p = 16
(b.) 1 + 1 = p – 1
(c.) p² – 4 = 0
(d.) 3p² = 48
(e.) p + p + p + p + p = 5

Matematika, Sekolah Menengah Atas

Jawab:

(a.) p = 4

(b.) 3 = p

(c.) p = 2

(d.) p = 4

(e.) p = 1

Penjelasan dengan langkah-langkah:

(a.) 4p = 16

Untuk mendapatkan nilai p dari persamaan ini, kita kalikan kedua ruas kanan dan kiri dengan 1/4, maka:

4p x 1/4 = 16 x 1/4 kita dapatkan hasil p:

p = 4

(b.) 1 + 1 = p – 1

Untuk mendapatkan nilai p dari persamaan ini, kita pindahkan angka -1 ke ruas kiri, menjadi:

1 + 1 = p – 1

2 = p – 1

2 + 1 = p

3 = p

(c.) p² – 4 = 0

Untuk mendapatkan nilai p dari persamaan ini, kita tambahkan kedua ruas dengan angka 4, kemudian hasilnya kita dapatkan akar dari angka perpindahan ruas tersebut:

p² – 4 = 0

p² = 4

p =

p = 2

(d.) 3p² = 48

Untuk mendapatkan nilai p dari persamaan ini, kita kalikan kedua ruas dengan 1/3, maka:

3p² x 1/3 = 48 x 1/3

p² = 16

p =

p = 4

(e.) p + p + p + p + p = 5

Untuk mendapatkan nilai p dari persamaan ini, kita jumlahkan semua p yang berada di ruas kiri, lalu kita kalikan kedua ruas dengan 1/5, maka akan kita dapatkanlah nilai p:

p + p + p + p + p = 5

5p = 5 lalu kita kalikan kedua ruas dengan 1/5:

5p x 1/5 = 5 x 1/5

p = 1

Semoga membantu ya.

3. sudut 15° berada pada kuadran .. a. I
b. II
c. III
d. IV
e. V

4. sudut 250° berada pada kuadran . .
a.I
b. II
c. III
d. IV
e. V

Matematika, Sekolah Menengah Atas

Jawab :

3. Sudut 15° berada pada kuadran I karena kurang dari 90° (a)

4. Sudut 250° berada pada kuadran III karena lebih dari 180° namun kurang dari 270° (c)

Quick note :

Kuadran I berkisar antara 0° < α < 90°

Kuadran II berkisar antara 90° < α < 180°

Kuadran III berkisar antara 180° < α < 270°
Kuadran IV berkisar antara 270° < α < 360°

Soal :

5! × 50
50 – 32 + 21
7!

otw hapus.

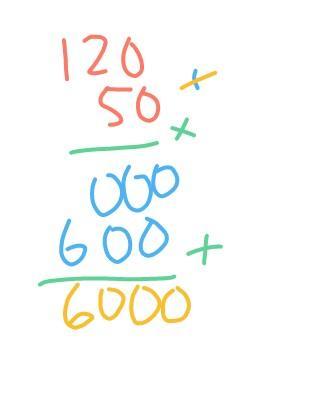
Matematika, Sekolah Menengah Pertama

Penjelasan dengan langkah-langkah:

5! × 50 = ?

= ( 5.4.3.2.1 ) × 50

= 120 × 50

= 6.000

50 – 32 + 21 = ?

= 50 – 32 + 21

= 18 + 21

= 39

7! = ?

= ( 7.6.5.4.3.2.1 )

= 5.040

—

Soal 1

—

5! × 50

(5 × 4 × 3 × 2 × 1) × 50

(20 × 3 × 2 × 1) × 50

(60 × 2 × 1) × 50

(120 × 1) × 50

120 × 50

6.000

—

Soal 2

—

50 – 32 + 21

18 + 21

—

Soal 3

—

7 × 6 × 5 × 4 × 3 × 2 × 1

42 × 5 × 4 × 3 × 2 × 1

210 × 4 × 3 × 2 × 1

840 × 3 × 2 × 1

2.520 × 2 × 1

5.040 × 1

5.040

—

Sebuah kubus mempunyai volume 14cm berapa volume kubus?

Matematika, Sekolah Menengah Atas

Penjelasan dengan langkah-langkah:

volume

s × s × s
14 × 14 × 14
196 × 14
2.744cm³

Jawaban:

Volume dari sebuah kubus tersebut adalah 2.744 cm³

✰▬▬▬▬▬▬▬※☠※▬▬▬▬▬▬▬✰

Pendahuluan:

Kubus merupakan salah satu bangun ruang yang memiliki sisi berbentuk persegi.

Macam-macam rumus kubus:

✮Volume

V=s³

=s×s×s

={…×…}×…

=…×…

=… cm³

✮Luas

L=6×s²

=6×{s×s}

=6×{…×…}

=6×…

=… cm²

✮Keliling

K=12×s

=12×…

=… cm

✰▬▬▬▬▬▬▬※☠※▬▬▬▬▬▬▬✰

Pembahasan:

V=s³

=s×s×s

={14×14}×14

=196×14

=2.744 cm³

✰▬▬▬▬▬▬▬※☠※▬▬▬▬▬▬▬✰

Detail:

Mapel:Matematika

Kelas:VI – 6

Tingkat:SD – Sekolah Dasar

Materi:Bab 4 – Bangun ruang

Kata kunci:Kubus,Volume

Kode soal:2

Kode:6.2.4

✰▬▬▬▬▬▬▬※☠※▬▬▬▬▬▬▬✰

#BelajarBersamaBrainly

#AyoBelajar

#TingkatkanPrestasimu

#BelajarDenganMiracle

Related Posts with Google CSEArtikel Terkait
    
  

❤Soal math❤ 5 poin je

Pendahuluan

Contoh soal

Detail Jawaban

— ‹ Pendahuluan

➳ Bilangan Eksponen Terdiri

— Bilangan Berpangkat Positif

— Bilangan Berpangkat Negatif

— Bilangan Berpangkat Nol

— Bilangan Berpangkat Dalam Bentuk Akar

______________________

❝ Contoh Bilangan Pangkat 2

______________________

❝ Contoh Bilangan Pangkat 3

______________________

❝ Sifat – Sifat Eksponen ‹

❝ Keterangan :

Pembahasan-! ꒰⑅꒱

– ᴋᴇsɪᴍᴘᴜʟᴀɴ:

______________________

— Pelajari Lebih Lanjut :

— Detail Jawaban:

Pertanyaan Baru di Matematika

Q. 146 – (-12) = (-23) + (-20) = “Sebenarnya yg hrs bil Terimakasih itu..kita atau penjual ny?,, klo kita bil mksh..kenapwa yg jualan ikut bil teyimakasih?” :v ​

∆Pembahasan∆

Jawaban:

➣Nomor 1:

➣Nomor 2:

Pendahuluan:

Pembahasan:

➣Nomor 1:

➣Nomor 2:

Detail:

Kuis: super mudah, yang duluan dpt BA Carilah nilai p dari persamaan-persamaan berikut ini. (a.) 4p = 16 (b.) 1 + 1 = p – 1 (c.) p² – 4 = 0 (d.) 3p² = 48 (e.) p + p + p + p + p = 5

3. sudut 15° berada pada kuadran .. a. Ib. IIc. IIId. IVe. V 4. sudut 250° berada pada kuadran . .a.Ib. IIc. IIId. IV e. V ​

Jawab :

Soal : 5! × 5050 – 32 + 217! otw hapus.​

Soal 1

Soal 2

Soal 3

Sebuah kubus mempunyai volume 14cm berapa volume kubus?​

Jawaban:

Pendahuluan:

Pembahasan:

Detail:

Artikel Terkait

Related Articles

Q. 146 – (-12) =

(-23) + (-20) =

“Sebenarnya yg hrs bil Terimakasih itu..kita atau penjual ny?,, klo kita bil mksh..kenapwa yg jualan ikut bil teyimakasih?” :v

Kuis: super mudah, yang duluan dpt BA Carilah nilai p dari persamaan-persamaan berikut ini.

(a.) 4p = 16
(b.) 1 + 1 = p – 1
(c.) p² – 4 = 0
(d.) 3p² = 48
(e.) p + p + p + p + p = 5

3. sudut 15° berada pada kuadran .. a. I
b. II
c. III
d. IV
e. V

4. sudut 250° berada pada kuadran . .
a.I
b. II
c. III
d. IV
e. V

Soal :

5! × 50
50 – 32 + 21
7!

otw hapus.

Sebuah kubus mempunyai volume 14cm berapa volume kubus?